If the non-parallel sides of a trapezium are equal, then
Given ABCD is a trapezium whose non-parallel sides AD and BC are equal.
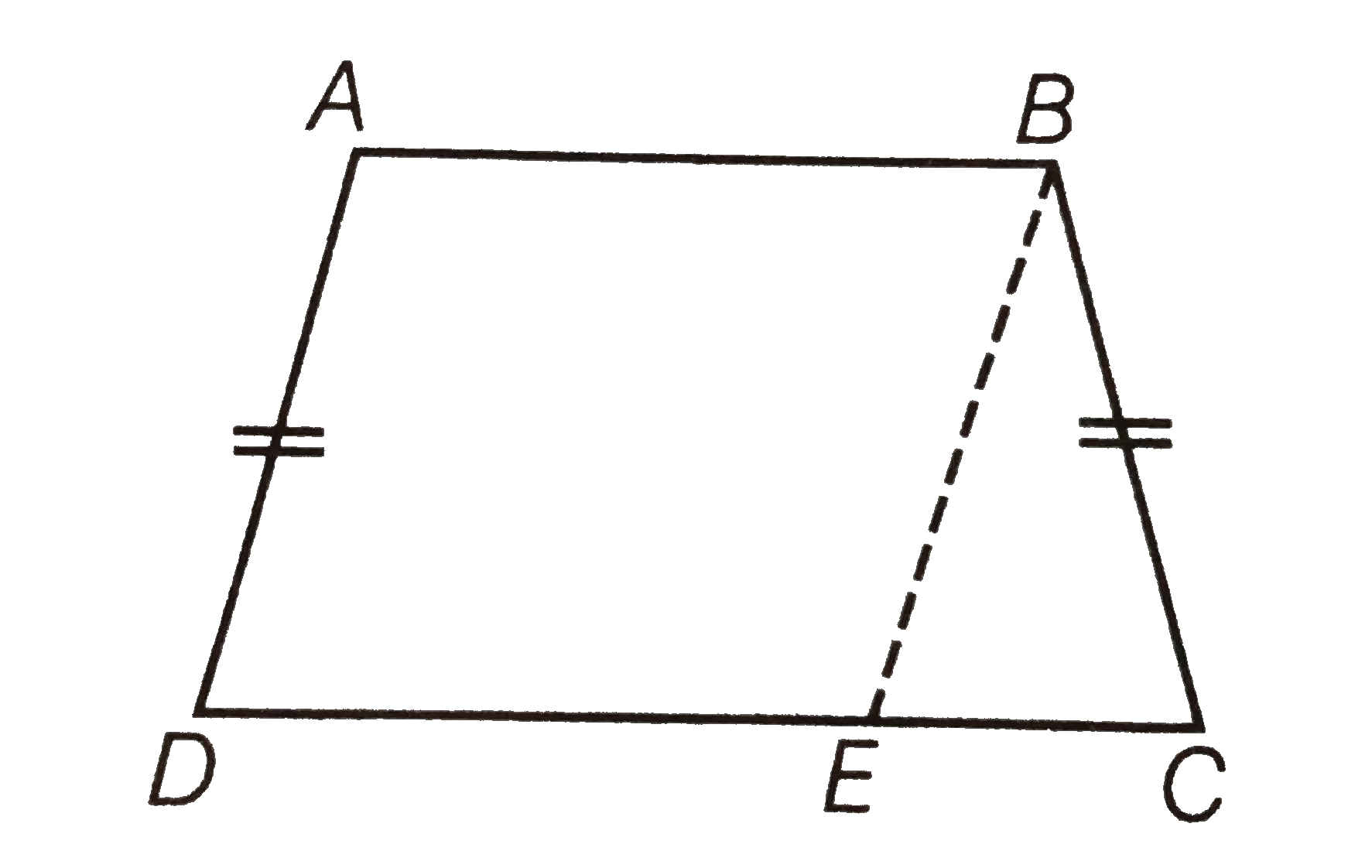
To prove Trapezium ABCD is a cyclic.
Join BE, where BE∣∣AD.
Proof Since, AB||DEandAD||BE
Since, the quadrilateral ABCD is a parallelogram.
∴∠BAD=∠BED ...(i)
[opposite angles of a parallelogram are equal]
and AD=BC ..(ii)
[opposite sides of a parallelogram are equal]
But AD=BC [given]...(iii)
From Eqs. (ii) and (iii), BC=BE
⇒∠BEC=∠BCE .....(iv)
[angles opposite to equal sides are equal]
Also, ∠BEC=∠BED=180∘ [linear pair axiom]
∴∠BCE+∠BAD=180∘ [from Eqs. (i) and (iv)]
If sum of opposite angles of a quaderilateral is 180∘, then quadrilateral is cyclic.
Hence, trapezium ABCD is a cyclic.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.42videos
CIRCLES
- BOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles34videos
Areas of Parallelograms and Triangles
- BOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions5videos
CONSTRUCTIONS
Similar Questions
If the non-parallel sides of a trapezium are equal, prove that it is cyclic.
View SolutionConsider the following statements :
1. If non-parallel sides of a trapezium are equal, then it is cyclic.
2. If the chord of a circle is equal to its radius, then the angle subtended by this chord at a point in major segment is 30∘.
Which of the above statements is/are correct?View Solution
Knowledge Check
- Question 1 - Select One
A trapezium inscribes a circle that touches all its sides and the line connecting the mid-points of the non-parallel sides of the trapezium divides the trapezium in such a way that the area of one part is half the area of the other part. If the lengths of the non-parallel sides be 8 cm and 16 cm, find the length of the shortest side of the trapezium.
A4B6C9Dnone of these - Question 2 - Select One
If the parallel sides of a trapezium are 8 cm and 4 cm, M and N are the mid points of the diagonals of the trapezium, then length of MN is
A12 cm.B6 cm.C1 cm.D2 cm.
If the non parallel sides of a trapezium are equal. Prove that it is cyclic.
View SolutionIf two non-parallel sides of a trapezium are equal; it is cyclic.
View SolutionIf two non-parallel sides of a trapezium are equal; it is cyclic.
View SolutionIf two non-parallel sides of a trapezium are equal, it is cyclic. OR An isosceles trapezium is always cyclic.
View SolutionProve that the segment joining the middle points of two non-parallel sides of a trapezium is parallel to the parallel sides and half of their sum.
View SolutionIf the parallel sides of a trapezium are 8 cm and 4 cm, M and N are the mid points of the diagonals of the trapezium, then length of MN is
View Solution

