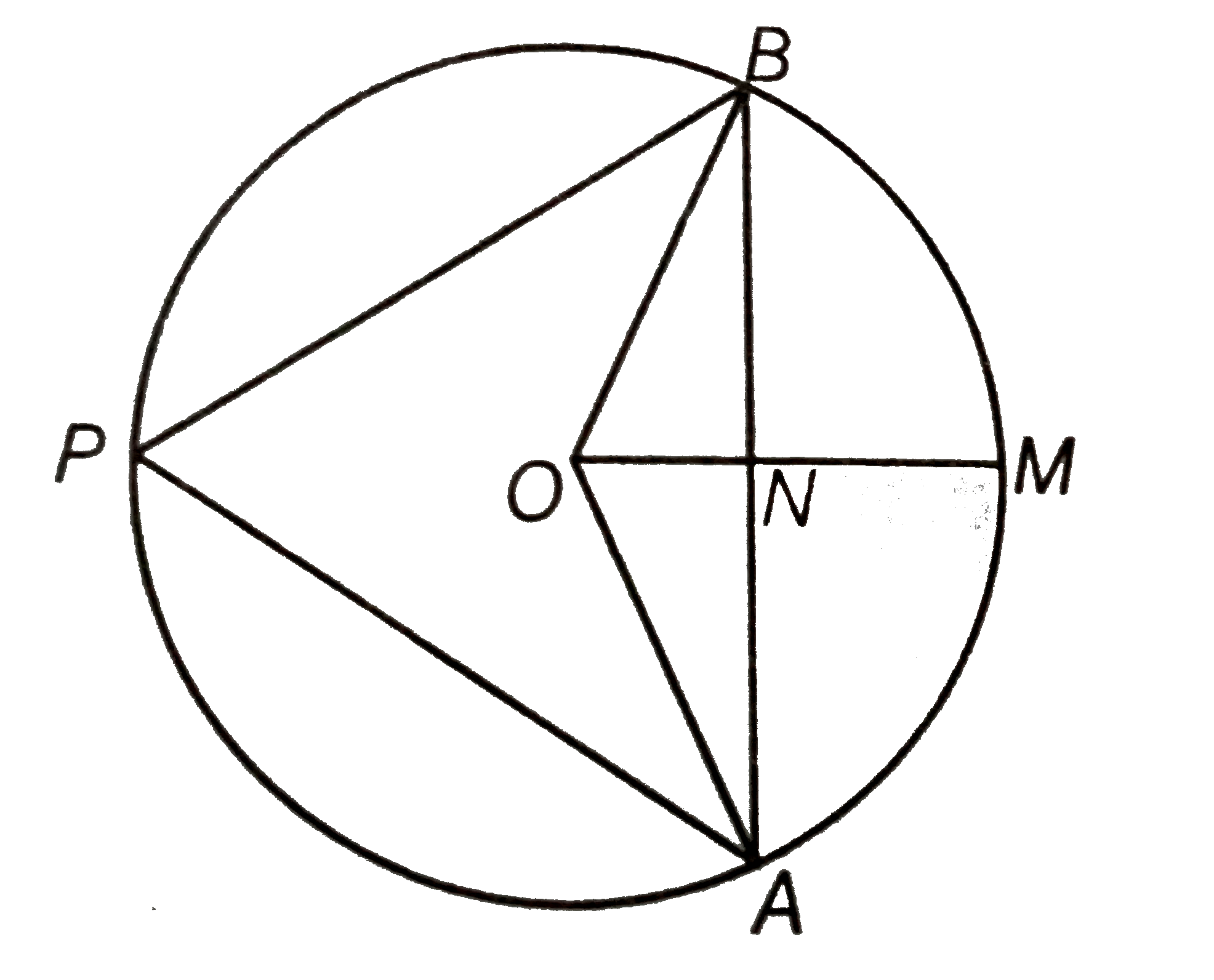
A circle has radius $\sqrt{2}$ cm it is divided into 2 segments by a chord of length 2cm prove that angle subtended by the chord at a point in major segment is $45^{\circ}$

Video Solution

Text Solution

Verified by Experts

Draw a circle having centre O. Let AB=2 cm be a chord of a circle. A chord AB is divided by the line OM in two equal segments.
To prove $∠ A P B = 45^{\circ}$
Here, AN=NB = 1 cm
and $O B = \sqrt{2} c m$
In $Δ O N B, O B^{2} = O N^{2} + N B^{2}$
[use Pythagoras theorem]
$\Rightarrow {(\sqrt{2})}^{2} = O N^{2} + {(1)}^{2}$
$\Rightarrow O N^{2} = 2 - 1 = 1$
$\Rightarrow O N = 1 c m$
[taking positive square root, because distance is always positive]
Also, $∠ O N B = 90^{\circ}$ [ON is the perpendicular bisector of the chord AB]
$∴ ∠ N O B = ∠ N B O = 45^{\circ}$
Similarly, $∠ A O N = 45^{\circ}$
Now, $∠ A O B = ∠ A O N + ∠ N O B$
$= 45^{\circ} + 45^{\circ} = 90^{\circ}$
We know that, chord subtends an angle to the circle is half the angle subtended by it to the centre.
$∴ ∠ A P B = \frac{1}{2} ∠ A O B$
$= \frac{90^{\circ}}{2} = 45^{\circ}$

Updated on:21/07/2023

If the chord of a circle is equal to the radius of the circle, then the angle subtended by the chord at a point on the minor arc is:
A $120^{\circ}$
B $150^{\circ}$
C $100^{\circ}$
D $110^{\circ}$
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc
A $150^{\circ}$
B $180^{\circ}$
C $160^{\circ}$
D $170^{\circ}$