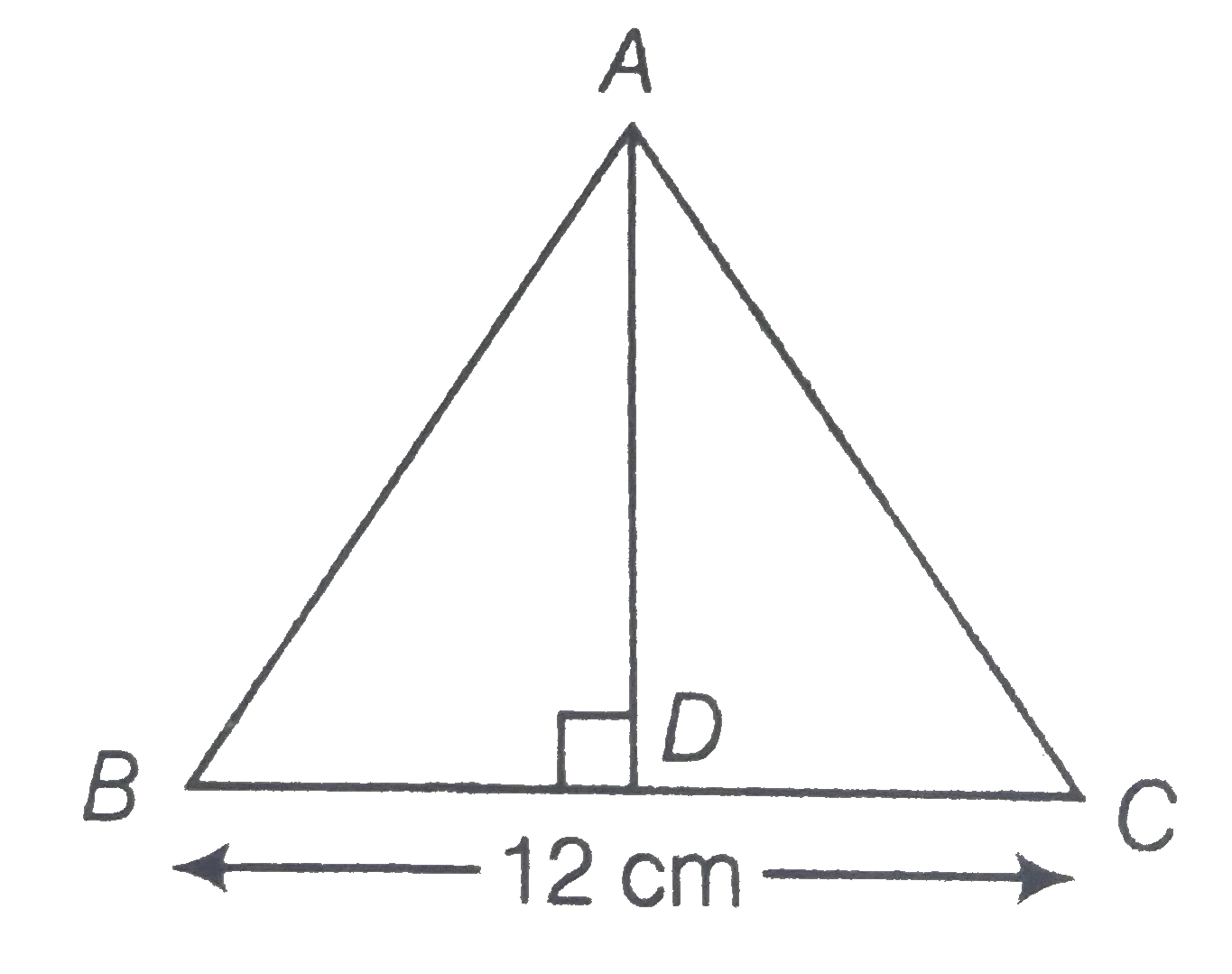
In a triangle, the sides are given as 11cm,12cm and 13cm. The length of the altitude is 10.25cm corresponding to the side having 12cm.
The correct Answer is:1
Since the sides of a triangle are a=11cm,b=12cm and c=13cm.
Now, semi-perimeter, s=a+b+c2
=11+12+132=362=18cm
Area of a triangle =√s(s−a)(s−b)(s−c) [by Heron's formula]
=√18(18−11)(18−12)(18−13)
=√18×7×6×5
=√3×6×7×6×5
6=√3×7×5
6=√105=6×10.25
61.5 cm2
∴ Area of△ABC=12×BC×AD [∵area of triangle=12(base×height)]
=12×12×10.25=6×10.25=61.5cm2
Topper's Solved these Questions
Similar Questions
Find the area of a triangle whose sides are 18cm,24cm and 30cm. Also find the length of altitude corresponding to the largest side of the triangle.
View SolutionCalculate the area of the triangle whose sides are 18 cm, 24 cm and 30 cm in length. Also, find the length of the altitude corresponding to the smallest side.
View Solution
Knowledge Check
The area of a triangle whose sides are 9 cm , 12 cm and 15 cm is
A54cm2B60cm2C64cm2DNone of theseFind the area of triangle whose sides are 17cm,8cmand15cm. Also calculate the length of the altitude corresponding to the largest side of the triangle.
A80cm2,7.06cmB50cm2,9.06cmC90cm2,7.06cmD60cm2,7.06cmThe sides of triangle are 13 cm, 14 cm and 15 cm. The area of the triangle is
A84cm2B91cm2C105cm2D97.5cm2
The sides of a triangle are 50 cm, 78 cm and 112 cm.The smallest altitude is
View SolutionThe sides of a triangle are 5 cm, 12 cm and 13 cm. Then its area is :
View SolutionThe lengths of the three sides of a triangle are 30 cm, 24 cm and 18 cm respectively. The length of the altitude of the triangle correspondihng to the smallest side is
View SolutionIn a triangle ABC, BC = 5 cm, AC = 12 cm and AB = 13 cm. The length of the altitude drawn from B on AC is -----
View SolutionThe lengths of three sides of a triangle are 20 cm, 16 cm and 12 cm. The area of the triangle is
View Solution
