Find the area of a parallelogram given in the figure. Also, find the length of the altitude from vertex $A$ on the side $D C$ .

Video Solution

Text Solution

Verified by Experts

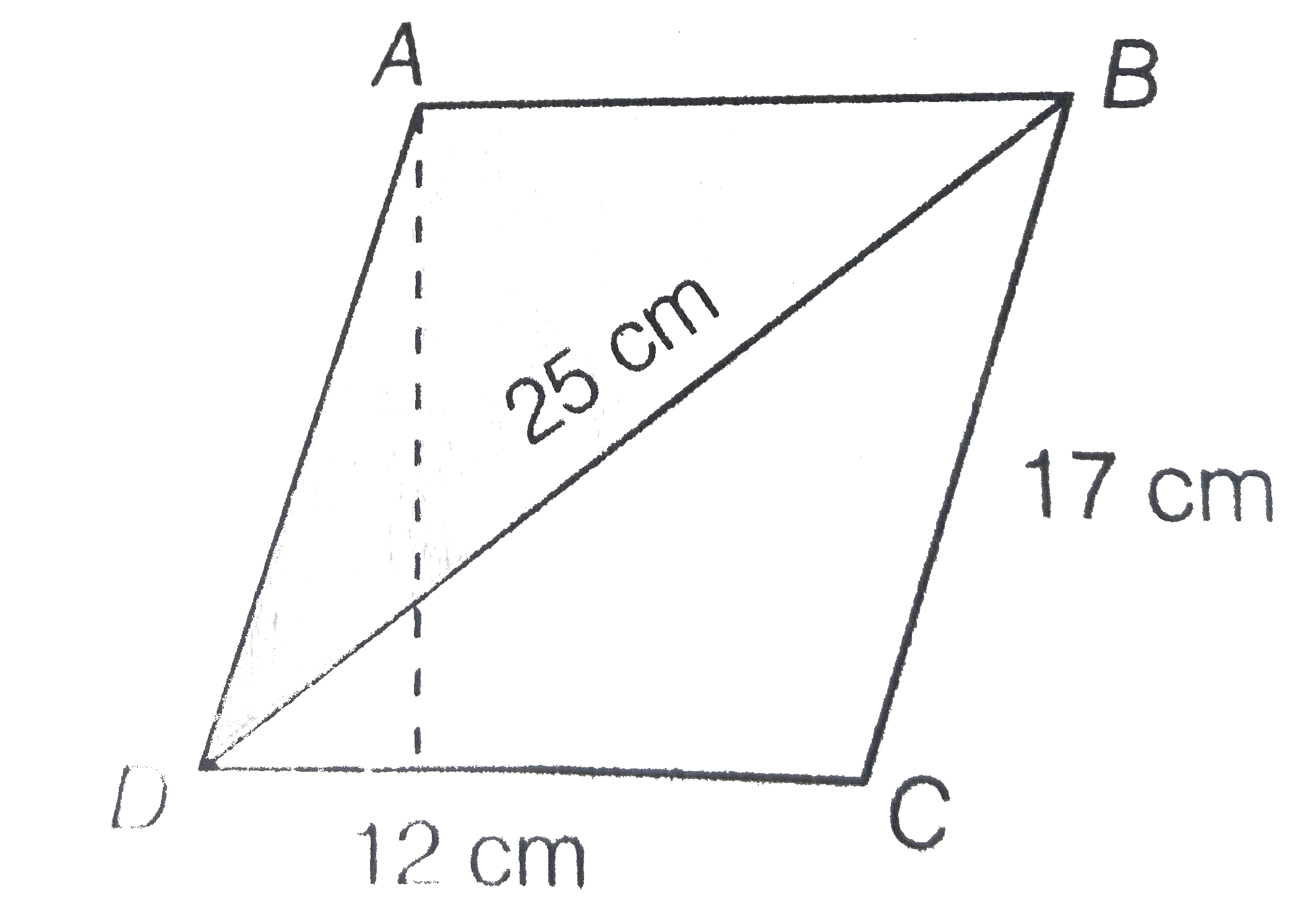
Area of parallelogram $A B C D = 2 (Area of △ B C D)$
Now, the sides of a $△ B C D$ are $a = 12 c m, b = 17 c m$ and $c = 25 c m .$
$∴ Semi-perimeter of △ B C D, s = \frac{a + b + c}{2} = \frac{12 + 17 + 25}{2} = \frac{54}{2} = 27 c m$
$∴ Area of △ B C D = \sqrt{s (s - a) (s - b) (s - c)} [by Heron's formula]$
$= \sqrt{27 (27 - 12) (27 - 17) (27 - 25)}$
$= \sqrt{27 \times 15 \times 10 \times 2}$
$= \sqrt{9 \times 3 \times 3 \times 5 \times 5 \times 2 \times 2}$
$= 3 \times 3 \times 5 \times 2 = 90 c m^{2}$
From Eq.(i),
Area of parallelogram $A B C D = 2 \times 90$
$= 180 c m^{2}$
Let altitude of parallelogram be h.
Also, area of parallelogram $A B C D = B a s e \times A < i t u d e$
$\Rightarrow 180 = D c \times h$
$\Rightarrow 180 = 12 \times h$
$∴ h = \frac{180}{12} = 15 c m$
Hence, the area of parallelogram is 180 $c m^{2}$ and the length of altitude is $15 c m .$

|

Updated on:21/07/2023

Class 9 MATHS HERONS FORMULA

Topper's Solved these Questions

Similar Questions

NCERT EXEMPLAR-HERON'S FORMULA-Herons Formula

Home
Ask Doubt
Profile