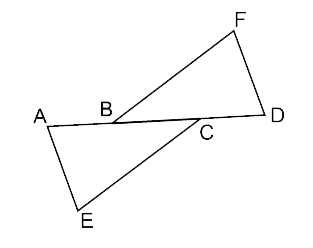
In the given figure, ∠ABD=∠GFD. CE bisects BF. Prove that ∠C=∠E.
Step by step video & image solution for In the given figure, /_ABD = /_GFD. CE bisects BF. Prove that /_C = /_E. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
In the given figure , AB=CD,CE=BF and ∠ACE==∠DBF . Prove that
AE=DF
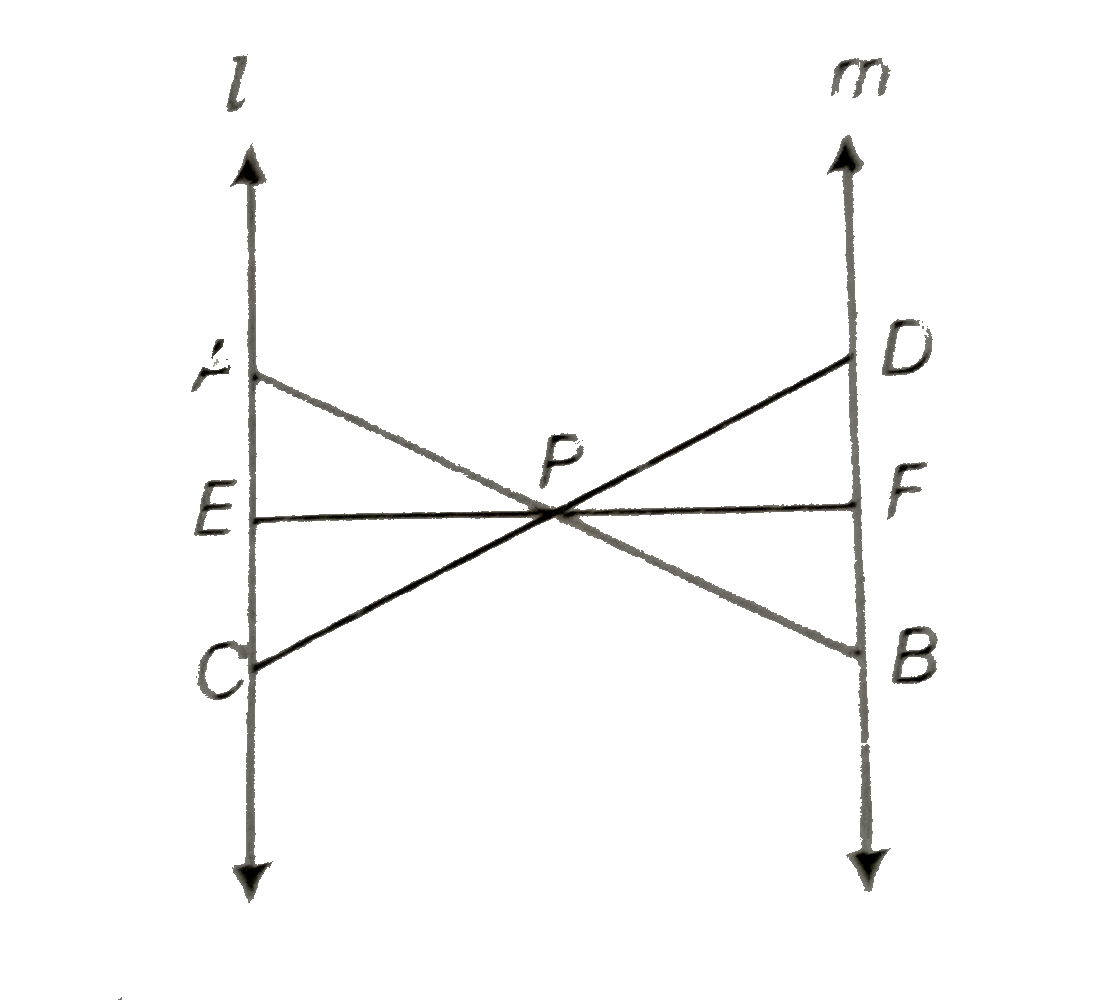
View SolutionIn given figure,l||m and liner segments AB, CD and EF are concurrent at point P. Prove that AEBF=ACBD=CEFD
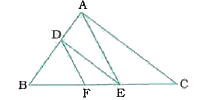
View SolutionIn the given figure, DE||AC and DF||AE . Prove that (BF)/(FE)=(BE)/(EC)
View SolutionIn Figure, AE bisects ∠CAD and ∠B=∠C. Prove that AE∣∣BC
View SolutionIn Figure, ∠E>∠A and ∠C>∠D . Prove that AD>EC
View SolutionIn the given figure, AC⊥CE and ∠A:∠B:∠C=3:2:1, find the value of ∠ECD.
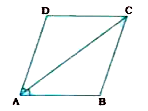
View SolutionDiagonal AC of a parallelogram ABCD bisects ∠A (see the given figure), show that :
it bisects ∠C also,
View SolutionIn the given figure, DE||AC and DF||AE. Prove that BFFE=BEEC
View Solution
