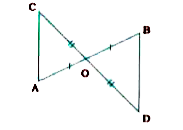
In given figure,l||m and liner segments AB, CD and EF are concurrent at point P. Prove that AEBF=ACBD=CEFD
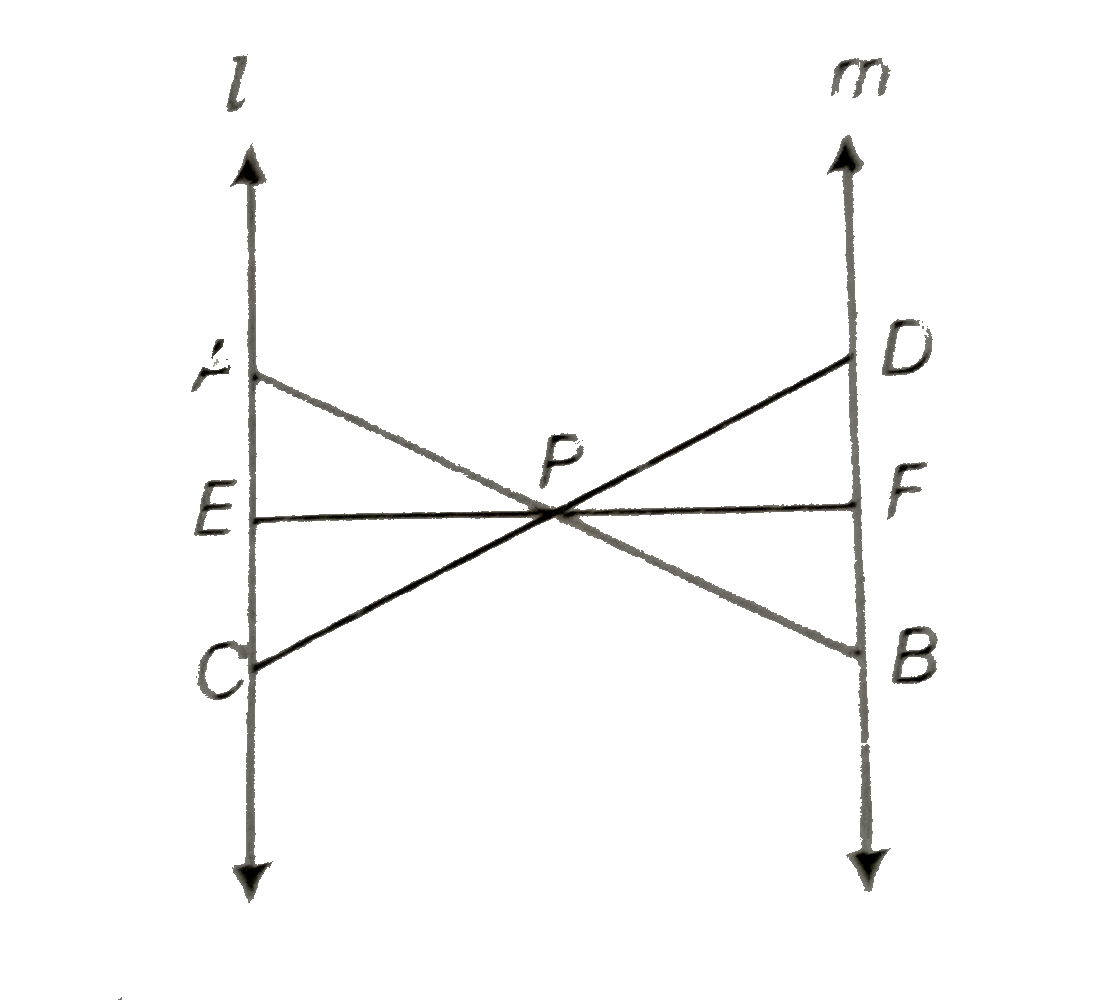
Given l||m and line segments AB, CD and EF are concurrent at point P
To prove AEBF=ACBD=CEFD
Proof In ΔAPCandΔBPD,∠APC=∠BPD [vertically opposite angle]
∠PAC=∠PBD [alternate angle]
∴ΔAPC~ΔBPD [by AAA similarity criterion]
Then, APPB=ACBD=PCPD
In ΔAPE and ΔBPF,∠APE=∠BPF [vertically opposite angles]
∠PAE=∠PBF [alternate angles]
∴ΔAPE~ΔBPF [by AAA similarity criterion]
Then, APPB=AEBF=PEPF....(ii)
In ΔPECandΔPFD,∠EPC=∠FPD [vertically opposite angle]
∠PCE=∠PDF [alternate angles]
∴ΔPEC~ΔPFD [by AAA similarity criterion]
Then, PEPF=PCPD=ECFD....(iii)
From Eqs. (i) ,(ii) and (iii),
APPB=ACBD=AEBF=PEPF=ECFD
∴AEBF=ACBD=CEFD Hence proved
Topper's Solved these Questions
Similar Questions
In the given figure, AB CD and EF are three lines concurrent at O. Find the value of y.
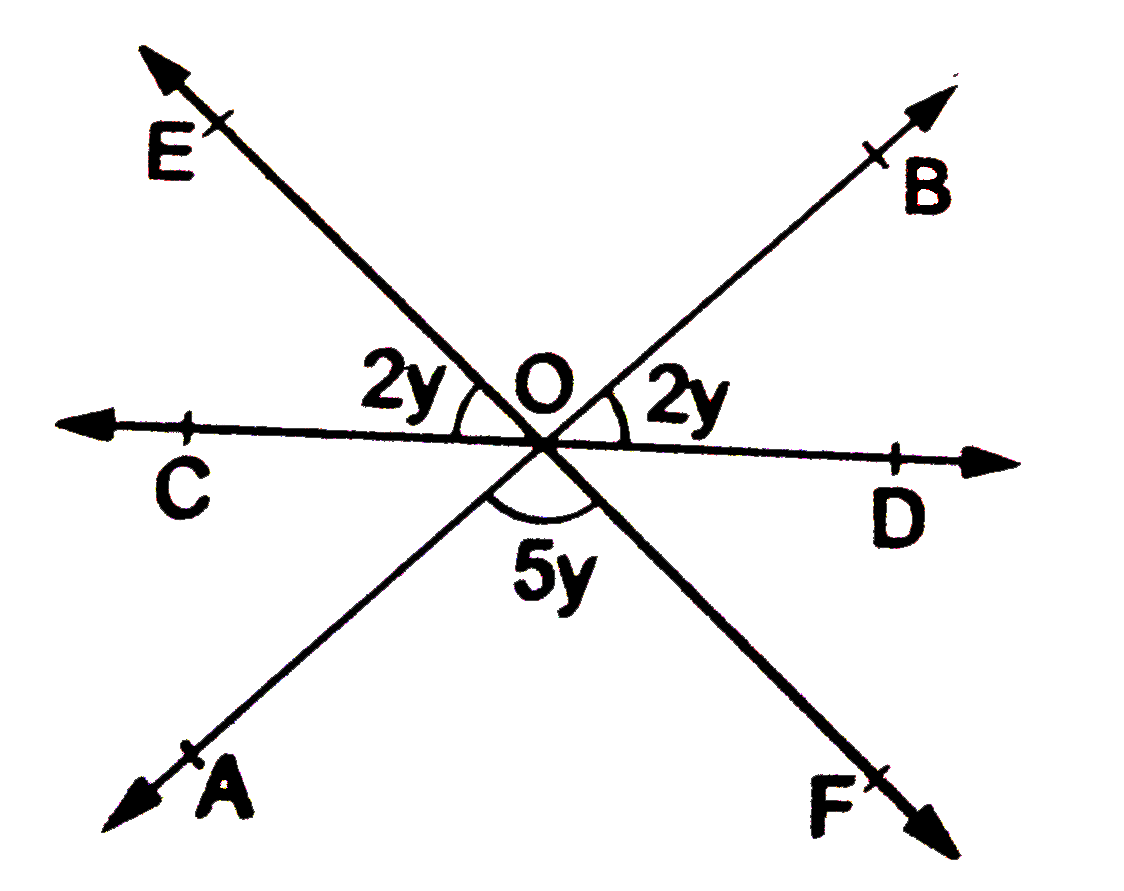 View Solution
View SolutionIn the given figure, ΔABC is an isosceles triangle in which AB=AC and AE bisects ∠CAD. Prove that AE∣∣BC.
View SolutionIn Fig. 4.104, if BD⊥AC and CE⊥AB , prove that (FIGURE) AECADB (ii) CAAB=CEDB
View SolutionIn trapezium AC and BD intersect each other at point P. Then prove that A(ΔABP)A(ΔCPD)=AB2CD2.
View SolutionIn an isoscles ΔABC,AB=ACandD is a point on BC. Prove that AB2−AD2=BD⋅CD.
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)
 View Solution
View SolutionIn Figure, ABC is an isosceles triangle with AB=AC, BD and CE are two medians of the triangle. Prove that BD=CE
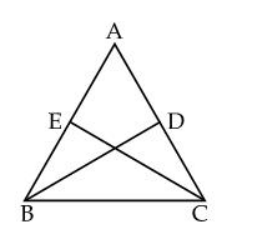 View Solution
View SolutionIn Figure, AD=AE and D and E are points on BC such that BD=EC. Prove that AB=AC
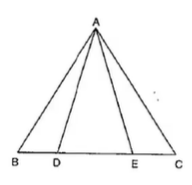 View Solution
View SolutionIn the given figure, DE||ACandDF||AE.
Prove that BFFE=BEEC
 View Solution
View SolutionIn the given figure AB and CD bisect each other at O. Prove that AC = BD.
 View Solution
View Solution

