Find the probability distribution of the maximum of two scores obtained when a die is thrown twice. Determine also the mean of the distribution.
To solve the problem of finding the probability distribution of the maximum of two scores obtained when a die is thrown twice, and to determine the mean of that distribution, we can follow these steps:
Step 1: Identify Possible Outcomes
When a die is thrown twice, the possible outcomes for each die are 1, 2, 3, 4, 5, and 6. Therefore, the total number of outcomes when throwing two dice is 6×6=36.
Step 2: Determine the Maximum Values
We need to find the probability distribution of the maximum score, which can take values from 1 to 6. We will calculate the probability for each maximum value.
Step 3: Calculate Probabilities for Each Maximum Value
1. Maximum = 1:
- The only way to achieve a maximum of 1 is if both dice show 1.
- Favorable outcomes: (1,1) → 1 outcome.
- Probability: P(X=1)=136.
2. Maximum = 2:
- The maximum can be 2 if both dice show either 1 or 2.
- Favorable outcomes: (1,1), (1,2), (2,1), (2,2) → 3 outcomes.
- Probability: P(X=2)=336=112.
3. Maximum = 3:
- The maximum can be 3 if at least one die shows 3 and none show higher.
- Favorable outcomes: (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3) → 5 outcomes.
- Probability: P(X=3)=536.
4. Maximum = 4:
- The maximum can be 4 if at least one die shows 4 and none show higher.
- Favorable outcomes: (1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4), (3,1), (3,2), (3,3), (3,4), (4,1), (4,2), (4,3), (4,4) → 7 outcomes.
- Probability: P(X=4)=736.
5. Maximum = 5:
- The maximum can be 5 if at least one die shows 5 and none show higher.
- Favorable outcomes: (1,1), (1,2), (1,3), (1,4), (1,5), (2,1), (2,2), (2,3), (2,4), (2,5), (3,1), (3,2), (3,3), (3,4), (3,5), (4,1), (4,2), (4,3), (4,4), (4,5), (5,1), (5,2), (5,3), (5,4), (5,5) → 9 outcomes.
- Probability: P(X=5)=936=14.
6. Maximum = 6:
- The maximum can be 6 if at least one die shows 6.
- Favorable outcomes: (1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6) → 11 outcomes.
- Probability: P(X=6)=1136.
Step 4: Summarize the Probability Distribution
The probability distribution of the maximum score X is as follows:
| X | Probability P(X) |
|-------|------------------------|
| 1 | 136 |
| 2 | 336 |
| 3 | 536 |
| 4 | 736 |
| 5 | 936 |
| 6 | 1136 |
Step 5: Calculate the Mean of the Distribution
To find the mean E(X), we use the formula:
E(X)=∑(x⋅P(X))
Calculating each term:
E(X)=1⋅136+2⋅336+3⋅536+4⋅736+5⋅936+6⋅1136
Calculating each product:
- 1⋅136=136
- 2⋅336=636
- 3⋅536=1536
- 4⋅736=2836
- 5⋅936=4536
- 6⋅1136=6636
Now summing these values:
E(X)=1+6+15+28+45+6636=16136
Final Result
Thus, the mean of the distribution is:
E(X)=16136
When a die is thrown twice, the possible outcomes for each die are 1, 2, 3, 4, 5, and 6. Therefore, the total number of outcomes when throwing two dice is 6×6=36.
We need to find the probability distribution of the maximum score, which can take values from 1 to 6. We will calculate the probability for each maximum value.
- The only way to achieve a maximum of 1 is if both dice show 1.
- Favorable outcomes: (1,1) → 1 outcome.
- Probability: P(X=1)=136.
- The maximum can be 2 if both dice show either 1 or 2.
- Favorable outcomes: (1,1), (1,2), (2,1), (2,2) → 3 outcomes.
- Probability: P(X=2)=336=112.
- The maximum can be 3 if at least one die shows 3 and none show higher.
- Favorable outcomes: (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3) → 5 outcomes.
- Probability: P(X=3)=536.
- The maximum can be 4 if at least one die shows 4 and none show higher.
- Favorable outcomes: (1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4), (3,1), (3,2), (3,3), (3,4), (4,1), (4,2), (4,3), (4,4) → 7 outcomes.
- Probability: P(X=4)=736.
- The maximum can be 5 if at least one die shows 5 and none show higher.
- Favorable outcomes: (1,1), (1,2), (1,3), (1,4), (1,5), (2,1), (2,2), (2,3), (2,4), (2,5), (3,1), (3,2), (3,3), (3,4), (3,5), (4,1), (4,2), (4,3), (4,4), (4,5), (5,1), (5,2), (5,3), (5,4), (5,5) → 9 outcomes.
- Probability: P(X=5)=936=14.
- The maximum can be 6 if at least one die shows 6.
- Favorable outcomes: (1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,1), (2,2), (2,3), (2,4), (2,5), (2,6), (3,1), (3,2), (3,3), (3,4), (3,5), (3,6), (4,1), (4,2), (4,3), (4,4), (4,5), (4,6), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6) → 11 outcomes.
- Probability: P(X=6)=1136.
The probability distribution of the maximum score X is as follows:
|-------|------------------------|
| 1 | 136 |
| 2 | 336 |
| 3 | 536 |
| 4 | 736 |
| 5 | 936 |
| 6 | 1136 |
To find the mean E(X), we use the formula:
- 2⋅336=636
- 3⋅536=1536
- 4⋅736=2836
- 5⋅936=4536
- 6⋅1136=6636
Thus, the mean of the distribution is:
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Obtain the mean of the following distribution.
 A7.5B8.05C9DNone
A7.5B8.05C9DNone
Determine the mean of the following distribution:
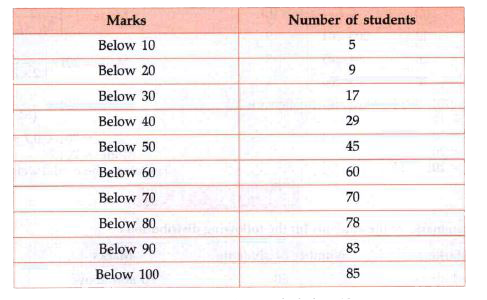 View Solution
View SolutionFind the mean of the following distribution.
 View Solution
View SolutionFind the mean of the following distribution.
 View Solution
View SolutionFind the probability distribution of the number of sixes in three tosses of a die.
View SolutionFind the mean of following distribution
 View Solution
View SolutionFind the mean of the following distribution
View SolutionFind the mean of the following distribution
 View Solution
View Solution



