A random variable X as the following probability distribution: xi:−2−10123 pi:0.1k0.22k0.3k Find (i) Find the value of k. (ii) Calculate the mean ofX. Calculate the variance of X.
Given that a random variable x has the following probability distribution
X=x∣−2,−1,0,1,23
p(x)∣0.1,k,0.2,2k,0.3,k
We know that in a probability total probability is unity
i.e∑p(x)=1
⇒0.1+k+0.2+2k+0.3+k=1
⇒0.6+4k=1
⇒4k=1−0.6=0.4
⇒4k=0.4
⇒k=0.44
=0.1
then probability distribution is value of k=0.1
Topper's Solved these Questions
Similar Questions
A random variable X as the following probability distribution: xi:−2−10123 pi:0.1k0.22k0.3k Find (i) Find the value of k. (ii) Calculate the mean ofX. Calculate the variance of X.
View SolutionA random variable X has the following probability distribution find K.
 View Solution
View SolutionA random variable X has the follwing probability distribution:

Find k.View SolutionA random variable X has the following probability distribution: Values of X: −2 −1 0 1 2 3 P(X):0.1 k 0.2 2k 0.3 k
View SolutionA random variable X has the follwing probability distribution:

Find P(0<X<4)View SolutionA random variable X has the following probability distribution:Determine (i) k (ii) P(X<3)(iii) P(X>6) (iv) P(0<X<3)
View SolutionA random variable X has the following probability distribution: X=xi: 1 2 3 4 P(X=xi): k 2k 3k 4k Write the value of P(X≥3) .
View SolutionA random variable X has the following probability distribution:
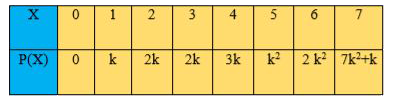
Determine : (i) k (ii) P(X<3) (iii) P(X>4)View SolutionA random variable X has the following probability distribution:
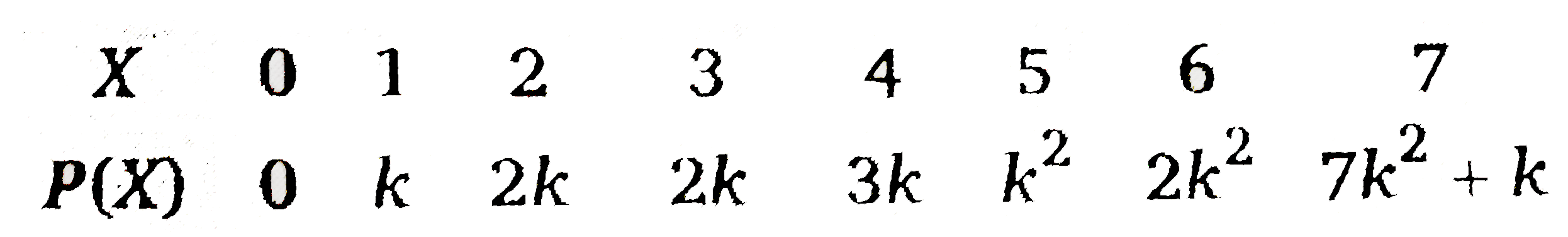
Determine :
(i) k
(ii) P(X<3)
(iii) P(X>6)
(iv) P(0<X<3)View SolutionA random variable 'X' has the following probability distribution :

Find : (i) the value of K (ii) P(X≤1)
(iii) P(X≥0).View Solution

