If z satisfies |z−1|+|z+1|=2, then locus of z is
A
A straight line passing through z=1 & z=-1
B
Circle
C
A line segment
D
Ellipse
Video Solution
Text Solution
The correct Answer is:1
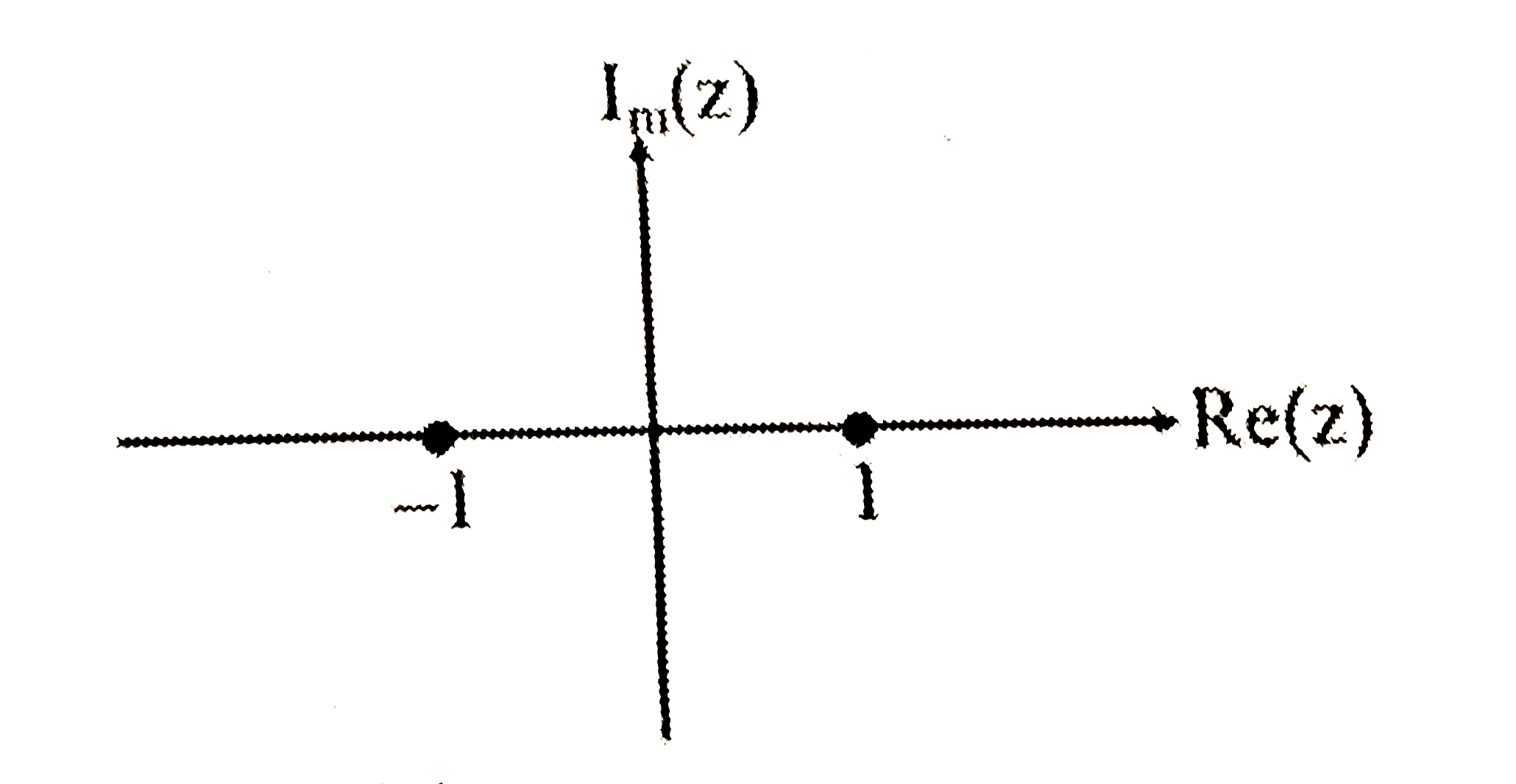
|z−1|and|z+1| represent distance of complex No. of z from 1 and -1 respectively in the Argand plane Now distance between z=-1 and z=1 is 2 & |z−1|+|z+1|=2 so locus will be line segment joining -1 & 1.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
If Im(z−12z+1)=−4, then locus of z is
Aan ellipseBa parabolaCa straight lineDa circleif |z−1|=|z−i| then locus of z is
Aa circle of radius 1Ba circle of radius 12CA straight line passing through origin with slope 1Da straight line passing through origin with slope −1If lm(z−12z+1)=−4 then locus of z is
AAn ellipseBA parabolaCA straight lineDA circle
If z satisfies |z−6+4i|+|z−3+2i|=13, then the locus of z is
View Solutionif |z+1|2+|z|2=4, then the locus of z is
View SolutionIf z2z−1 is always real, then locus of z is
View SolutionIf Real (2z−1z+1)=1, then locus of z is , where z=x+iy and i=√−1
View SolutionIf z=x+iy and real part (z−12z+1)=1 then locus of z is
View Solution
