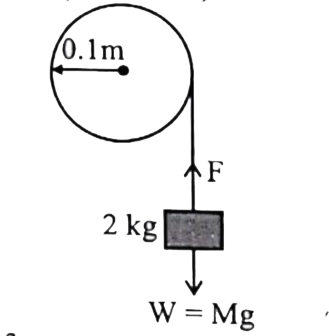
The moment of inertia of a solid flywheel about its axis is $0.1 k g - m^{2}$ .A tangential force of 2 kg-wt. is applied round the circumference of the flywheel with the help of a string and mass arrangement as shown in the figure. If the radius of the wheel is 0.1 m, find the acceleration $({in rad/sec}^{2})$ of the mass :

A

163.3

B

16.3

C

81.66

D

8.16

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$a = \frac{m g}{m + I / r^{2}} = \frac{19.6}{12}$
$α = \frac{a}{R} = 16.33 r a d / s^{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If moment of inertia of a solid sphere of mass 5kg about its diameter is $50 k g m^{2}$ . Its moment of inertia about its tangent in kg $m^{2}$ is
A260
B250
C240
D175
Question 2 - Select One
The moment of inertia of a disc of radius 0.5m about its geometric axis is 2kg- $m^{2}$ . If a string is tied to its circumference and a force of 10 Newton is applied, the value of torque with respect to this axis will be:
A2.5 N-m
B5 N-m
C10 N-m
D20 N-m
Question 3 - Select One
the angular acceleration of flywheel having moment of inertia 50 kg $m^{2}$ when a torque of 5 $N - m$ is applied on the flywheel is
A $20.1 r a d s^{- 2}$
B $250 r a d s^{- 2}$
C $10 r a d s^{- 2}$
D $1.25 r a d s^{- 2}$

CAREER POINT-UNIT TEST 3-PHYSICS

Home
Ask Doubt
Profile