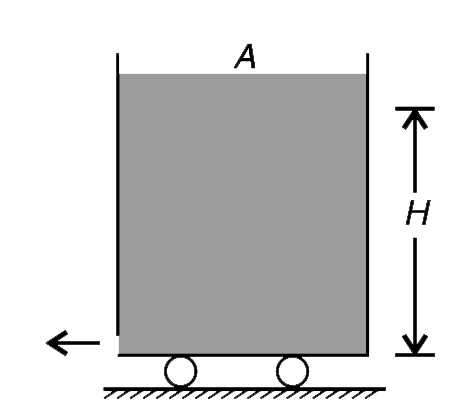
A vertical tank, open at the top, is filled with a liquid and rests on

A tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :

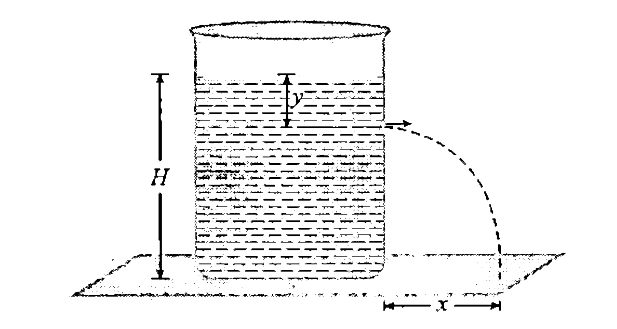AIF y is increased from zero to H, x will first increase and then decrease
Bx is maximum for $y = H / 2$
CThe maximum value of x is H
DThe maximum value of x will depend on the density of the liquid
A rectangular tank is placed on a horizontal ground and is filled with water to a height H above the base. A small hole is made on one vertical side at a depth D below the level of the water in the tank. The distance x from the bottom of the tank at which the water jet from the tank will hit the ground is
A $2 \sqrt{D (H - D)}$
B $2 \sqrt{D H}$
C $2 \sqrt{D (H + D)}$
D $\frac{1}{2} \sqrt{D H}$
Choose the most appropriate option.
A tank is filled with a liquid upto a height H. A small hole is made at the bottom of this tank. Consider $t_{1}$ be the time taken to empty first half of the tank and $t_{2}$ be the time taken to empty rest half of the tank. Then, determine the ratio $\frac{t_{1}}{t_{2}}$ .
A1.33
B1.5
C2
D0.414

A tank, which is open at the top, contains a liquid up to a height H. A small hole is made in the side of the tank at a distance y below the liquid surface. The liquid emerging from the hole lands at a distance x from the tank :