A beaker containing a liquid of density $ρ$ moves up with an acceleration $a$ . The pressure due to the liquid at a depth h below the free surface of the liquid is.

A

$h ρ g$

B

$h ρ (g + a)$

C

$h ρ (g - a)$

D

$2 h ρ g (\frac{g - a}{g + a})$

Video Solution

|

Answer

Step by step video & image solution for A beaker containing a liquid of density rho moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS FLUID

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The pressure in a liquid at a given depth below the surface :
Ais always exerted downward.
Bis the same in all directions .
Cequals the total weight of liquid above the depth.
Ddepends upon the amount of liquid below the depth .
Question 2 - Select One
A hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density $ρ$ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is

A(a) $M g$
B(b) $M g - V ρ g$
C(c) $M g + π R^{2} h ρ g$
D(d) $ρ g (V + π R^{2} h)$
Question 3 - Select One

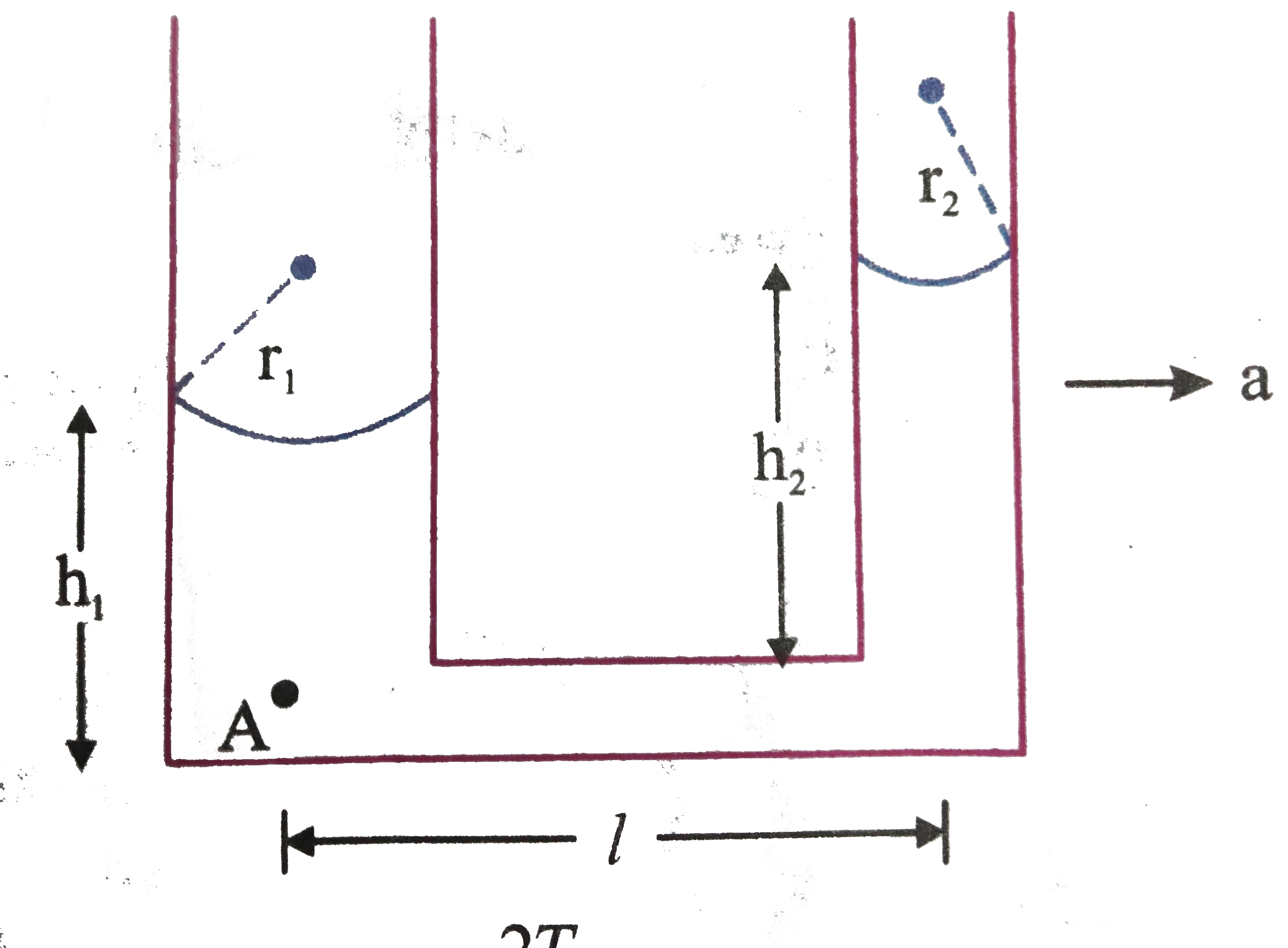
A vertical communicating tube contains a liquid of density $ρ$ . If it moves with a horizontal acceleration $a$ , pressure at $A$ is equal to :
A $ρ g h_{2} + P_{0} + \frac{2 T}{r_{2}} + ρ a l$
B $ρ g h_{2} + ρ a l + P_{0} - \frac{2 T}{r_{2}}$
C $ρ g h_{1} + P_{0} - \frac{2 T}{r_{1}}$
D $ρ g h_{1} - P_{0} - \frac{2 T}{r_{1}}$

MOTION-FLUID-Exercise-2 (level-I)

Home
Ask Doubt
Profile