In the previous question instead of spherical wall there is a vertical wall at a perpendicular distance d from the point & where the light is incident.

tanθ=xd
⇒x=dtanθ
dxdt=dsec2θdθdt
=2ωdsec∘θ (∵dθdt=2ω)
OR
Considering an instantaneus cricle of radius dsecθ.
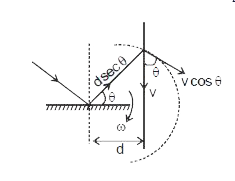
vt=2ωdsecθ
(2ωscosθ is a component of v.)
vcosθ=2ωdsecθ
⇒v=2ωsecθcosθ=2ωdsec2θ
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 1 Section A - Plane Mirror
12 Videos
- GEOMETRICAL OPTICSBOOK - MOTIONCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise - 1 Section B, C, D, E - Mirror formula and Magnification, Velocity in Spherical Mirror, Cutting of Mirrors, Combination of Mirrors, Intensity of light
10 Videos
- FLUIDBOOK - MOTIONCHAPTER - FLUIDEXERCISE - Exercise-4 level-II
5 Videos
- GRAVITATIONBOOK - MOTIONCHAPTER - GRAVITATIONEXERCISE - Exercise - 4 Section - B Previous Years Problems
15 Videos
Similar Questions
A sphere of radius R is supported by a rope attached to the wall. The rope makes an angle θ=45∘ with respect to the wall. The point where the rope is attached to the wall is at a distance of 3R2 from the point where the sphere touches the wall. Find the minimum coefficient of friction (μ) between the wall and the sphere for this equilibrium to be possible.
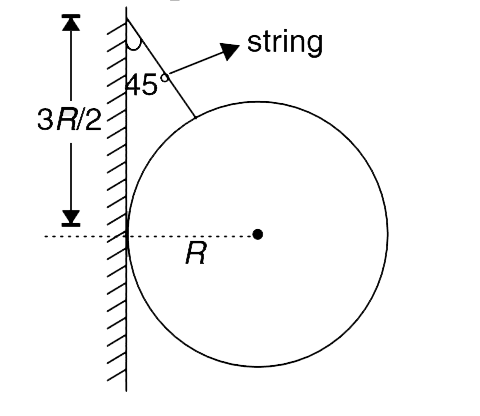
View SolutionA small ball is projected with a velocity u at some angle with horizontal towards a smooth vertical wall at a distance d from the point of projection after rebounding from the wall . If e is the coefficient of restitution then find maximum distance d for which ball may return to point of projection .
View Solution
Knowledge Check
As shown below AB represents an infinite wall tangential to a horizontal semi-circular track. O is a point source of light on the ground at the centre of the circle. A block moves along the circular track with a speed v starting from the point where the wall touches the circle. If the velocity and acceleration of shadow along the length of the wall is respectively V and a, then :
 AV=vcos(vtR)BV=vsec2(vtR)Ca=(v2R)sec2(vtR)tan(vtR)Da=(2v2R)sec2(vtR)tan(vtR)
AV=vcos(vtR)BV=vsec2(vtR)Ca=(v2R)sec2(vtR)tan(vtR)Da=(2v2R)sec2(vtR)tan(vtR)As shown in figure AB represents an infinite wall tangential to a horizontal semi circular track.O is a point source of light on the ground at the centre of the circle. A block moves along the circular track with speed v starting from the point where the wall touches the circle. If the velocity and acceleration of shadow along the length of the wall is respectively 'V' and 'a' then,
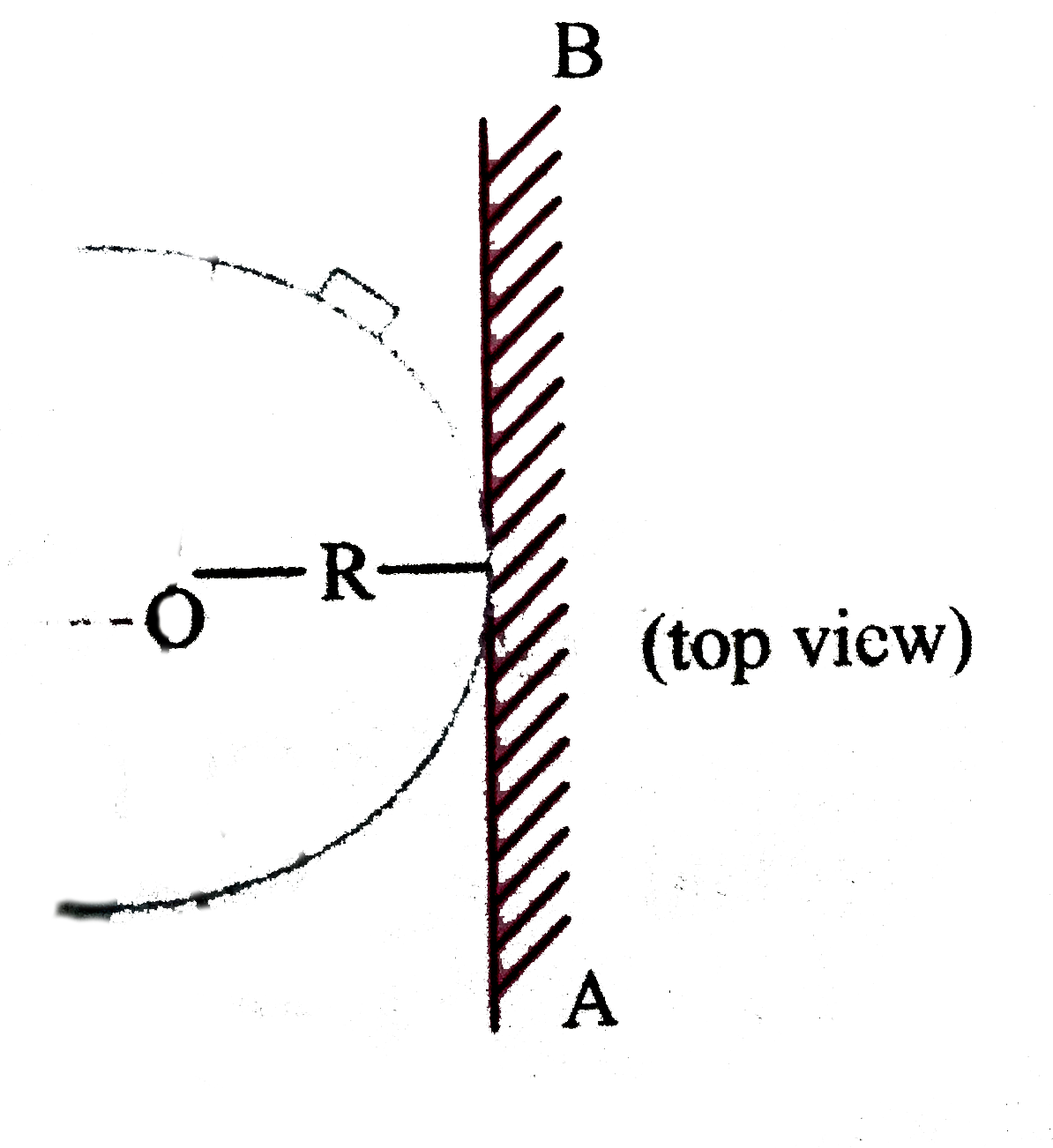 AV=vcosvtRBV=vsec2(vtR)Ca=v2Rsec2(vtR)tan(vtR)Da=2v2Rsec2(vtR)tan(vtR)
AV=vcosvtRBV=vsec2(vtR)Ca=v2Rsec2(vtR)tan(vtR)Da=2v2Rsec2(vtR)tan(vtR)A ladder rests against the side of a wall and reaches a point that is h meters above the ground. The angle formed by the ladder and the ground is θ∘. A point on the ladder is k meters from the wall.What is the vertical distance, in meters, from this point on the ladder to the ground?
A(h−k)tanθ∘B(h−k)cosθ∘Ch−ksinθ∘Dh−ktanθ∘
A ball is projected from ground with a speed 70m/s at an angle 45∘ with the vertical so that it strikes a vertical wall at horizontal distance 4903m from the point of projection. If the ball returns back to the poin tof projection without any collision with ground then find the coefficient of restitution between the ball and wall.
View SolutionA ball is projected from ground with a speed 70m/s at an angle 45∘ with the vertical so that it strikes a vertical wall at horizontal distance 4903m from the point of projection. If the ball returns back to the poin tof projection without any collision with ground then find the coefficient of restitution between the ball and wall.
View SolutionConsider a thick walled metallic spherical shell with inner radius a and outer radius b. No charge is given to the spherical shell. A point charge +Q is kept at the centre. Find the electric potential at a point distance x from the centre where 0<x<∞.
View SolutionTwo candles of equal height h are placed in between vertical walls on a line perpendicular to the walls at a distance a from each other and also from the nearer wall. With what speed will the shadows of the candles move along the walls if one burns out completely in time t1 and the other in time t2.
View SolutionA ball is projected from a given point with velocity u at some angle with the horizontal and after hitting a vertical wall returns to the same point. Show that the distance of the point from the wall must be less than eu2(1+e)g, where e is the coefficient of restitution.
View Solution
