A cylinder of radius R1 have cylinderical cavity of radius R2 as shown in the figure and have current density J (down ward). Find Magnetic field when
when point is in cavity
To find the magnetic field at a point inside a cylindrical cavity of a cylinder with a uniform current density, we can follow these steps:
1. Understand the Setup:
- We have a solid cylinder of radius R1 with a cylindrical cavity of radius R2.
- The current density J is directed downwards throughout the cylinder, including the cavity.
2. Superposition of Current Densities:
- To find the magnetic field inside the cavity, we can use the principle of superposition.
- We consider the effect of the current density J in the entire cylinder and then subtract the effect of the current density that would have been present in the cavity if it were filled with the same current density.
3. Magnetic Field Inside a Cylinder:
- The magnetic field B inside a uniformly current-carrying cylinder at a distance r from the center is given by:
B=μ0Jr2
- Here, μ0 is the permeability of free space.
4. Calculate Magnetic Field Contributions:
- For the solid cylinder (without the cavity), at a point inside the cavity (which is at radius R2):
B1=μ0JR12
- For the cavity (if it were filled with current density J):
B2=μ0(−J)R22
- The negative sign indicates that the current density in the cavity is opposite to the current density in the surrounding material.
5. Combine the Magnetic Fields:
- The total magnetic field B at a point inside the cavity is the sum of B1 and B2:
B=B1+B2=μ0JR12+μ0(−J)R22
- Simplifying this, we get:
B=μ0J2(R1−R2)
6. Conclusion:
- The magnetic field inside the cavity is:
B=μ0J2(R1−R2)
- This equation gives the magnetic field at any point inside the cavity.
- We have a solid cylinder of radius R1 with a cylindrical cavity of radius R2.
- The current density J is directed downwards throughout the cylinder, including the cavity.
- To find the magnetic field inside the cavity, we can use the principle of superposition.
- We consider the effect of the current density J in the entire cylinder and then subtract the effect of the current density that would have been present in the cavity if it were filled with the same current density.
- The magnetic field B inside a uniformly current-carrying cylinder at a distance r from the center is given by:
B=μ0Jr2
- Here, μ0 is the permeability of free space.
- For the solid cylinder (without the cavity), at a point inside the cavity (which is at radius R2):
B1=μ0JR12
- For the cavity (if it were filled with current density J):
B2=μ0(−J)R22
- The negative sign indicates that the current density in the cavity is opposite to the current density in the surrounding material.
- The total magnetic field B at a point inside the cavity is the sum of B1 and B2:
B=B1+B2=μ0JR12+μ0(−J)R22
- Simplifying this, we get:
B=μ0J2(R1−R2)
- The magnetic field inside the cavity is:
B=μ0J2(R1−R2)
- This equation gives the magnetic field at any point inside the cavity.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-150videos
MAGNETISM
- BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-2 (Level-I)40videos
MAGNETISM
- BOOK - MOTIONCHAPTER - LOGIC GATESEXERCISE - EXERCISE - 210videos
LOGIC GATES
- BOOK - MOTIONCHAPTER - MAGNETISM -1EXERCISE - Exercise - 3 SECTION -A56videos
MAGNETISM -1
Similar Questions
A cylinder of radius R1 have cylinderical cavity of radius R2 as shown in the figure and have current density J (down ward). Find Magnetic field when
r>R1 (on x-axis towards right)
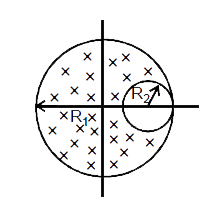 View Solution
View SolutionThere is a long cylinder of radius R having a cylindrical cavity of radius R/2 as shown in the figure. Apart from the cavity, the entire space inside the cylinder has a uniform mag- netic field parallel to the axis of the cylinder. The magnetic field starts changing at a uniform rate of dBdt=kT/s. Find the induced electric field at a point inside the cavity.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One

An infinity long cylinder of radius R has an infinitely long cylindrical cavity of radius R2 are shown in the figure. The remaining portion has uniform volume charge density ρ. The magnitude of electrical field at the centre of the cavity is-AρR6ε0BρR4ε0CρR2ε0DρR3ε0 - Question 2 - Select One
From a cylinder of radius R, a cylider of radius R/2 is removed, as shown in Fig. Current flowing in the remaining cylinder is I. Then, magnetic field strength is
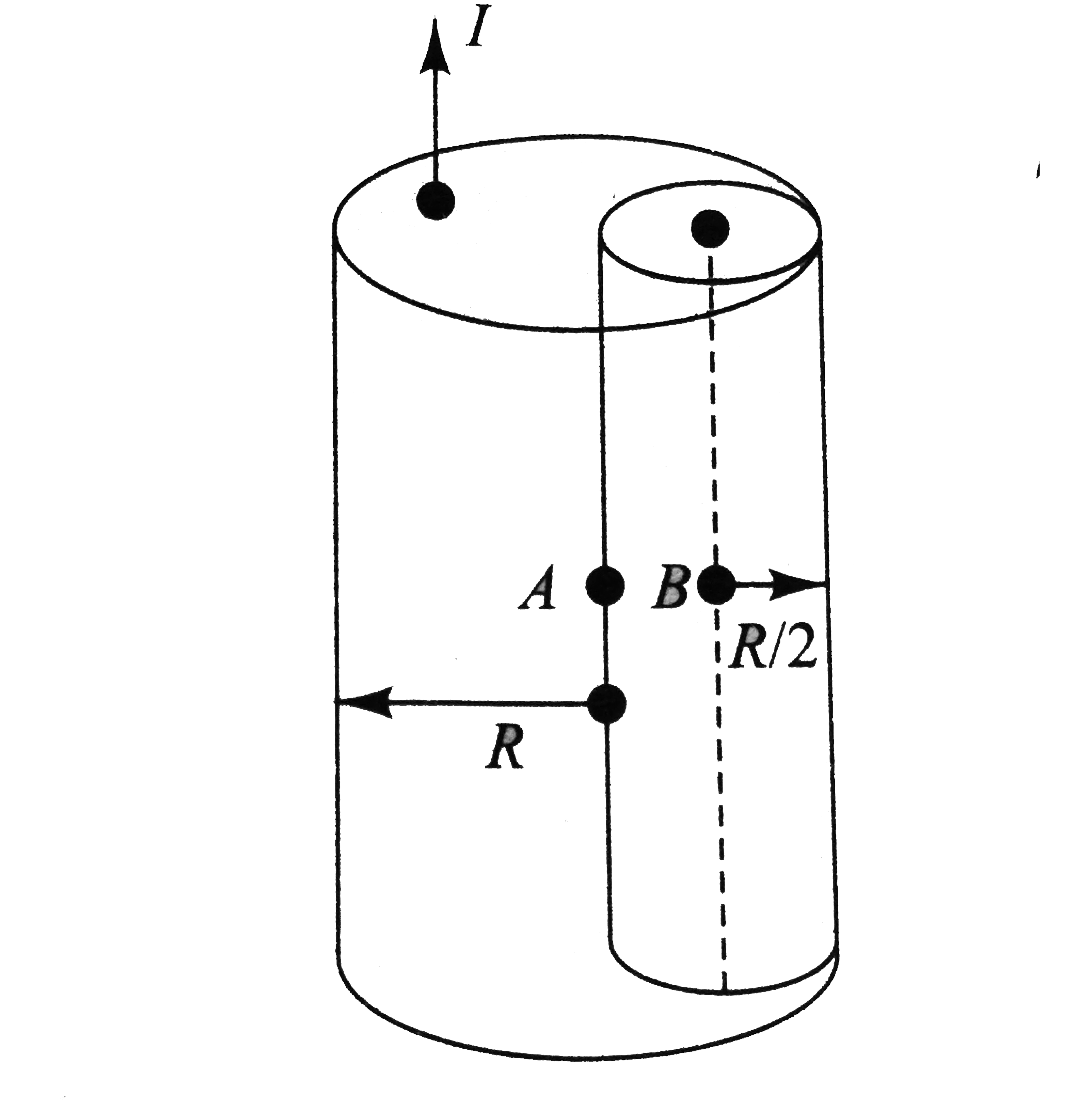 Aμ0I3πR at point BBμ0I2πR at point ACzero at point BDzero at point A
Aμ0I3πR at point BBμ0I2πR at point ACzero at point BDzero at point A - Question 3 - Select One
A solid sphere of radius R has a spherical cavity of radius r as shown in the figure. If the volume charge density σ is uniformly distributed over the whole volume of the sphere, then electric field strength at the centre of the sphere will be
 AR3σ2πε0(R−r)2BRσ3πε0C13ε0r3σ(R−r)2Drσ3ε0(R−r)2
AR3σ2πε0(R−r)2BRσ3πε0C13ε0r3σ(R−r)2Drσ3ε0(R−r)2
A circular metallic disc of radius R has a small circular cavity of radius r as shown in figure. On heating the system
 View Solution
View SolutionA circular metallic disc of radius R has a small circular cavity of radius r as shown in figure. On heating the system :
 View Solution
View SolutionA non-conducting sphere of radius R has a spherical cavity of radius R/2 as shown. The solid part of the sphere has a uniform volume charge density ρ. Find the magnitude and direction of electric field at point (a) O and (b) A.
 View Solution
View SolutionA hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then
 View Solution
View SolutionFrom a cylinder of radius R, a cyclinder of radius R/2 is removed, as shown . Current flowing in the remaning cylinder is l. magnetic field strength is :
 View Solution
View Solution

