Find potential at point A and B due to the small charge -system fixed near origin. (distance between the charges is negligible).
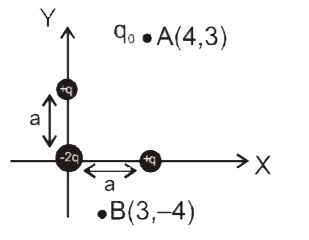
Dipole moment of the system is
→P=(qa)+(qa)ˆj
Potential at point A due to the dipole
VA=K(→P.→r)rB=K[(qa)ˆi+(qa)ˆj].(4ˆi+3ˆi)53=k(qa)125(7)
⇒VB=K[(qa)ˆi+(qa)ˆj](3ˆi−4ˆj)53=k(qa)125
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - SELF MISCELLANEOUS PROBLEM (Example )
15 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - SELF PRACTICE PROBLEM
27 Videos
- ELECTRONICS - SEMI CONDUCTORBOOK - MOTIONCHAPTER - ELECTRONICS - SEMI CONDUCTOREXERCISE - EXERCISE - 3
29 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
13 Videos
Similar Questions
(i) Find potential at point A and B sue to the small charge - system fixed near origin. (Distance between the charges is negligible).
(ii) Find work done to bring a test charge q0 from point A to point B, slowly. All parameters are in S.I. units.
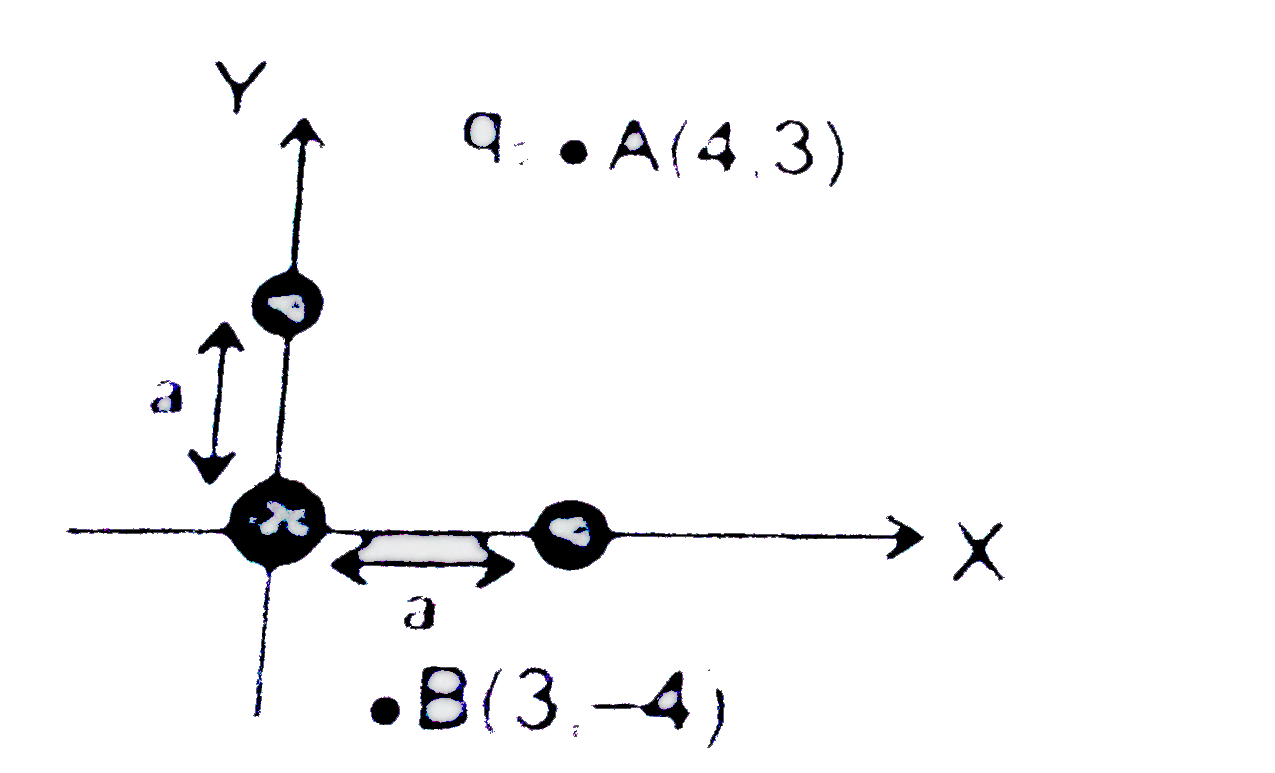
View Solution(i) Find potential at point A and B sue to the small charge - system fixed near origin. (Distance between the charges is negligible).
(ii) Find work done to bring a test charge q0 from point A to point B, slowly. All parameters are in S.I. units.

View Solution
Knowledge Check
Potential at a point due to a point charge is V. The charge is doubled and also the distance of the point from the charge is doubled. The new potential is
AV/2B4VCVD2VTwo point charges of same magnitude and opposite sign are fixed at point a and B. A third small point charge is to be balanced at point P by the electrostatic force due to these two charges. The point P :
 Alies on the perpendicular bisector of line ABBis at mid point of line ABClies to the left of ADnone of these
Alies on the perpendicular bisector of line ABBis at mid point of line ABClies to the left of ADnone of theseTwo positive point charges are separated by a distance R. If the distance between the charges is reduced to R/2, what happens to the total electric potential energy of the system?
AIt is doubledBIt is reduced to one-half of its original valueCIt remains the sameDIt is reduced to one-fourth of its original value
Value of potential at a point due to a point charge is
View SolutionFind an expression for the potential at a point due to a point charge Q.
View SolutionPotential Due To A Point Charge
View SolutionTwo point charges of same magnitude and opposite sign are fixed at point a and B. A third small point charge is to be balanced at point P by the electrostatic force due to these two charges. The point P :

View SolutionA charge +q is fixed at each of the points x=x0, x=3x0, x=5x0,…………x=∞ on the x axis, and a charge −q is fixed at each of the points x=2x0, x=4x0, x=6x0, …………x=∞. Here x0 is a positive constant. Take the electric potential at a point due to a charge Q at a distance r from it to be Q/(4πε0r).Then, the potential at the origin due to the above system of
View Solution
