Two charge 9e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is :
(r1+√3) from 9e charge
(r1+√1/3) from 9e charge
(r1−√3) from 3e charge
(r1+√1/3) from 3e charge
The correct Answer is:B
To find the distance from the charge 9e where the electric field intensity will be zero, we can follow these steps:
1. Identify the Charges and Their Positions:
- We have two charges: Q1=9e and Q2=3e.
- The distance between the two charges is r.
2. Set Up the Problem:
- We want to find a point where the electric field due to both charges cancels out. This point can either be between the charges or outside them.
3. Consider the Electric Field Directions:
- The electric field due to a positive charge points away from the charge.
- Therefore, the electric field due to Q1 (9e) will point away from it, and the electric field due to Q2 (3e) will also point away from it.
4. Assume a Point Between the Charges:
- Let x be the distance from the charge Q1 (9e) to the point where the electric field is zero.
- The distance from Q2 (3e) to this point will then be r−x.
5. Write the Expression for Electric Fields:
- The electric field E1 due to charge Q1 at distance x is given by:
E1=k⋅9ex2
- The electric field E2 due to charge Q2 at distance r−x is given by:
E2=k⋅3e(r−x)2
6. Set the Electric Fields Equal:
- For the electric field to be zero, the magnitudes of the electric fields must be equal:
9ex2=3e(r−x)2
7. Cancel Common Terms:
- We can cancel e and k from both sides:
9x2=3(r−x)2
8. Cross Multiply:
- Cross multiplying gives:
9(r−x)2=3x2
9. Expand and Rearrange:
- Expanding the left side:
9(r2−2rx+x2)=3x2
- Rearranging gives:
9r2−18rx+9x2−3x2=0
- This simplifies to:
9r2−18rx+6x2=0
10. Use the Quadratic Formula:
- This is a quadratic equation in x:
6x2−18rx+9r2=0
- Using the quadratic formula x=−b±√b2−4ac2a:
x=18r±√(−18r)2−4⋅6⋅9r22⋅6
x=18r±√324r2−216r212
x=18r±√108r212
x=18r±6√3r12
x=3r(3±√3)6=r(3±√3)2
11. Select the Positive Solution:
- Since x must be positive, we take the positive root:
x=r(3−√3)2
Final Answer:
The distance from the charge 9e where the electric field intensity will be zero is:
x=r(3−√3)2
- We have two charges: Q1=9e and Q2=3e.
- The distance between the two charges is r.
- We want to find a point where the electric field due to both charges cancels out. This point can either be between the charges or outside them.
- The electric field due to a positive charge points away from the charge.
- Therefore, the electric field due to Q1 (9e) will point away from it, and the electric field due to Q2 (3e) will also point away from it.
- Let x be the distance from the charge Q1 (9e) to the point where the electric field is zero.
- The distance from Q2 (3e) to this point will then be r−x.
- The electric field E1 due to charge Q1 at distance x is given by:
E1=k⋅9ex2
- The electric field E2 due to charge Q2 at distance r−x is given by:
E2=k⋅3e(r−x)2
- For the electric field to be zero, the magnitudes of the electric fields must be equal:
9ex2=3e(r−x)2
- We can cancel e and k from both sides:
9x2=3(r−x)2
- Cross multiplying gives:
9(r−x)2=3x2
- Expanding the left side:
9(r2−2rx+x2)=3x2
- Rearranging gives:
9r2−18rx+9x2−3x2=0
- This simplifies to:
9r2−18rx+6x2=0
- This is a quadratic equation in x:
6x2−18rx+9r2=0
- Using the quadratic formula x=−b±√b2−4ac2a:
x=18r±√(−18r)2−4⋅6⋅9r22⋅6
x=18r±√324r2−216r212
x=18r±√108r212
x=18r±6√3r12
x=3r(3±√3)6=r(3±√3)2
- Since x must be positive, we take the positive root:
x=r(3−√3)2
The distance from the charge 9e where the electric field intensity will be zero is:
x=r(3−√3)2
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise - 2 (Objective Problems | NEET)64videos
ELECTROSTATICS
- BOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (A)41videos
ELECTROSTATICS
- BOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - SELF PRACTICE PROBLEM27videos
ELECTROSTATICS
- BOOK - MOTIONCHAPTER - ELECTRONICS - SEMI CONDUCTOREXERCISE - EXERCISE - 329videos
ELECTRONICS - SEMI CONDUCTOR
- BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED13videos
ELECTROSTATICS - I
Similar Questions
Knowledge Check
- Question 1 - Select One
Two charges e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is
Ar(1+√3) from 3e chargeBr(1+√3) from e chargeCr(1−√3) from 3e chargeDr1+√13 from e charge - Question 2 - Select One
Two unequal and opposite charges are kept fixed at a distance. What is the number of points in space where electric Field intensity is zero due to this system?
A0B1C2DNone - Question 3 - Select One
Charges +2Q and −Q are placed as shown in figure. The point at which electric field intensity is zero will be
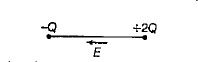 ASomewhere between −Q and +20BSomewhere on the left of −QCSomewhere on the right of +2QDSomewhere on the right bisector of line Joining−Q and +2Q
ASomewhere between −Q and +20BSomewhere on the left of −QCSomewhere on the right of +2QDSomewhere on the right bisector of line Joining−Q and +2Q
Charge 2Q and −Q are placed as shown in figure. The point at which electric field intensity is zero will be somewhere
 View Solution
View SolutionTwo charges of values 2μC and −50μC are placed at a distance of 6 cm from each other. The distance of the point (in cm) from the bigger charge where the electric intensity will be zero is :
View SolutionTwo charges of same polarity are kept fixed at a distance. What is the number of points in space where the electric field intensity due to this system is zero?
View SolutionTwo charge Q1=18μC and Q2=−2μC are separted by a distance R, and Q1 is on the left off Q2. The distance of the point where the net electric field is zero is
View SolutionTwo point masses having mass m and 2m are placed at distance d . The point on the line joining point masses , where gravitational field intensity is zero will be at distance
View Solution


