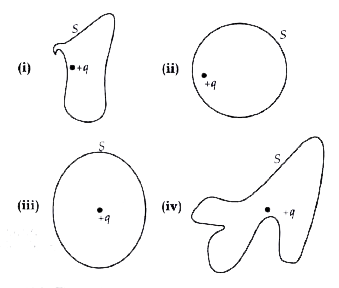A surface enclosed an electric dipole, the flux through the surface is -
Infinite
Positive
Negative
Zero
The correct Answer is:D
To find the electric flux through a surface enclosing an electric dipole, we can follow these steps:
1. Understand the Electric Dipole: An electric dipole consists of two equal and opposite charges, +q and -q, separated by a distance (let's say 2d).
2. Identify the Gaussian Surface: We consider a closed surface (Gaussian surface) that encloses the electric dipole.
3. Apply Gauss's Law: According to Gauss's law, the electric flux (Φ) through a closed surface is given by:
Φ=∮E⋅dA=Qenclosedϵ0
where Qenclosed is the total charge enclosed by the surface, and ϵ0 is the permittivity of free space.
4. Calculate the Enclosed Charge: In the case of an electric dipole, the total charge enclosed by the surface is:
Qenclosed=+q+(−q)=0
5. Determine the Electric Flux: Since the total enclosed charge is zero, we can substitute this into Gauss's law:
Φ=0ϵ0=0
6. Conclusion: Therefore, the electric flux through the surface enclosing the electric dipole is zero.
Final Answer:
The flux through the surface enclosing an electric dipole is 0.
---
Φ=∮E⋅dA=Qenclosedϵ0
where Qenclosed is the total charge enclosed by the surface, and ϵ0 is the permittivity of free space.
Qenclosed=+q+(−q)=0
Φ=0ϵ0=0
The flux through the surface enclosing an electric dipole is 0.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise - 2 (Objective Problems | NEET)
64 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (A)
41 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - SELF PRACTICE PROBLEM
27 Videos
- ELECTRONICS - SEMI CONDUCTORBOOK - MOTIONCHAPTER - ELECTRONICS - SEMI CONDUCTOREXERCISE - EXERCISE - 3
29 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
13 Videos
Similar Questions
Knowledge Check
The electric flux through the surface
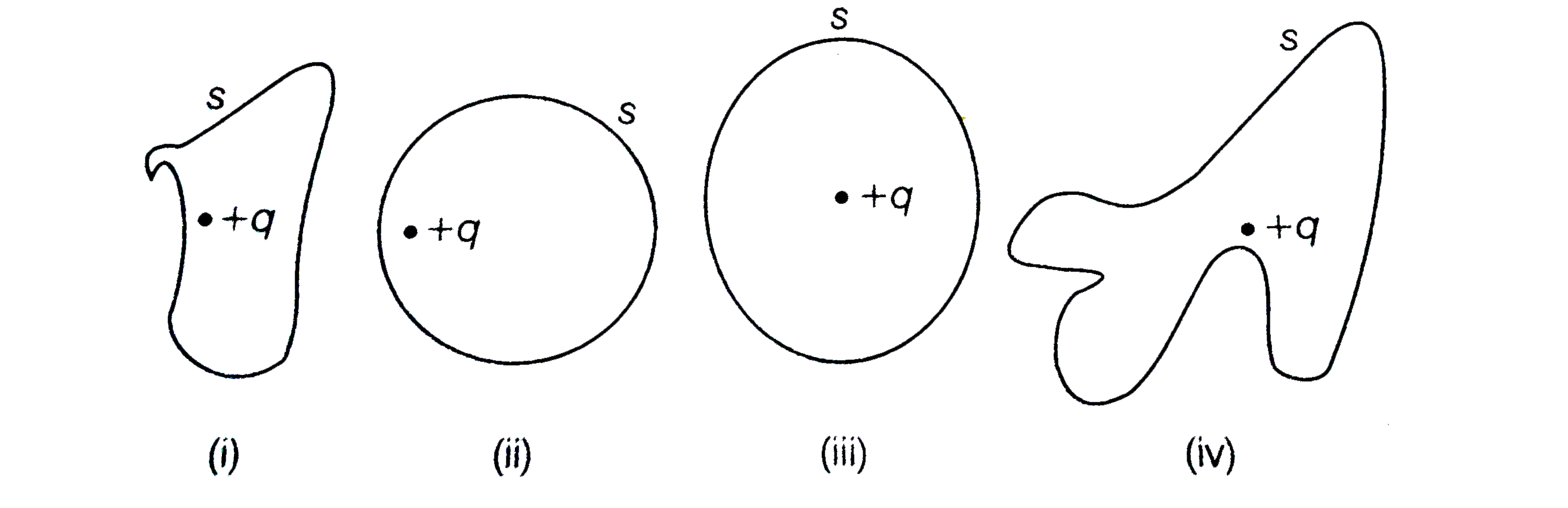 Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.
Ain fig. (iv) is the largestBin fig. (iii) is the leastCin fig. (ii) is same as fig.(iii) but is smaller than fig.(iv)DIs the same for all the figures.The electric flux through the surface
 Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.
Ain fig, (iv) is the largestBin fig, (iii) is the leastCin fig (ii) is same as a fig (iii) but is smaller than that in Fig (iv).Dis the same for all the figures.A cubical guassian surface encloses 24 C of charge. The electric flux through each surface of the cube is
A24ε0V−mB4ε0V−mC12ε0V−mD2.4ε0V−m
When a 10 μC charge is enclosed by a closed surface, the flux passing through the surface is ϕ. Now another 10 µC charge is placed inside the closed surface, then the flux passing through the surface is ______.
View SolutionA surface enclosed an electric dipole, the flux through the surface is -
View SolutionA plane surface of area 200cm2 is kept in a uniform electric field of intensity 200 N/C. if the angle between the normal to the surface and field is 60∘, the electric flux through the surface is
View SolutionAssertion: Electric flux represents the number of electric lines passing normally through the given surface in the electric field.
Reason: Electric flux through a surface is given as
ϕ=qε0
View SolutionA wire AB of length L has linear charge density λ=Kx, where x is measured from the end A of the wire. This wire is enclosed by a Gaussian hollow surface. Find the expression for electric flux through the surface.
View Solution