A body of mass 5 kg is suspended by the string making angles 60∘ and 30∘ with the horizontal
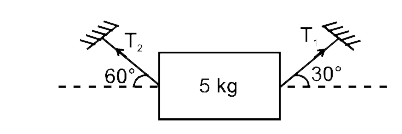
(a) T1=25N
(b) T2=25N
(c) T1=25√3N
(d) T2=25√3N
a, b
a, d
c, d
b, c
The correct Answer is:B
Step by step video, text & image solution for A body of mass 5 kg is suspended by the string making angles 60^(@) and 30^(@) with the horizontal (a) T_(1)=25N (b) T_(2)=25N (c) T_(1)=25sqrt(3)N (d) T_(2)=25sqrt(3)N by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 1 (SECTION-A:- String Constrained, Wedge Constrained, Newtons Law theory Question, Equillibrium Questions (Normal and Tension), Problems with Acceleration (F=ma), Wedge problems)27videos
NEWTON'S LAWS OF MOTION & FRICTION
- BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 1 SECTION-B :- Pulley Block System12videos
NEWTON'S LAWS OF MOTION & FRICTION
- BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Problem26videos
NEWTON'S LAWS OF MOTION & FRICTION
- BOOK - MOTIONCHAPTER - MODERN PHYSICS -1EXERCISE - EXERCISE-4 ( LEVEL- II)39videos
MODERN PHYSICS -1
- BOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-4 ( LEVEL-II)15videos
NLM & FRICTION
Similar Questions
A body of mass 5kg is suspended by the strings making angles 60∘ and 30∘with the horizontal -
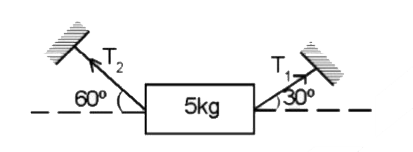
(a) T1=25N ( b) T2=25N
(c ) T1=25√3N (d) T2=25√3View SolutionAs body of mass 5 kg is suspended by the stirngs making angles 60∘ and 30∘ with the horizontal :
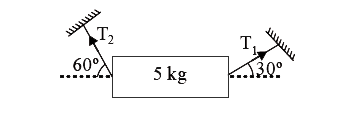
(a) T1=25N (b) T2=25N
( c ) T1=25√3N ( d ) T2=25√3NView Solution
Knowledge Check
- Question 1 - Select One
Three blocks are connected as shown in the figure
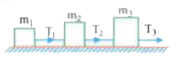
If m1=5kg,m2=10kgandm3=15kg, find the tension T1 given that T3=60NAZeroB45 NC30 ND10 N - Question 2 - Select One
In an A.P. if S1=T1+T2+T3+…+Tn (n odd) S2=T1+T3+T5+…+Tn, then S1/S2 =
A2nn+1Bnn+1Cn+12nDn+1n
Write the first two terms of the sequence
(i) tn=3n−6 (ii) tn=1n2−1View SolutionIf A>0, B>0 and A+B= π6 , then the minimum value of tanA+tanB is: 2−√3 b. 4−2√3 c. √3−√2 d. 2√3
View SolutionSum of the first n terms of an A.P. having positive terms is given by Sn=(1+2Tn)(1−Tn)(whereTn is the nth term of the series). The value of T22 is (A) √2+12√2 (B) √2−12√2 (C) 12√2 (D) none of these
View SolutionProve the trigonometric identities: If Tn=sinnθ+cosnθ, prove that T3−T5T1=T5−T7T3
View SolutionIf √5n=125, then 5n√64= 25 (b) 1125 (c) 625 (d) 15
View Solutionlimn→∞12+1+32+...+n225n2+n+3
View Solution

