A block of mass m resting on a wedge of angle θ as shown in the figure. The wedge is given an acceleration a. What is the minimum value of a so that the mass m falls freely ?
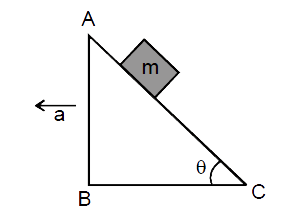
g
gcosθ
gcotθ
gtanθ
The correct Answer is:C
Step by step video, text & image solution for A block of mass m resting on a wedge of angle theta as shown in the figure. The wedge is given an acceleration a. What is the minimum value of a so that the mass m falls freely ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 1 SECTION-D :- Spring force and spring cutting problems
7 Videos
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 1 SECTION-E:- Static friction, Kinetic friction
13 Videos
- NEWTON'S LAWS OF MOTION & FRICTION BOOK - MOTIONCHAPTER - NEWTON'S LAWS OF MOTION & FRICTION EXERCISE - Exercise - 1 SECTION-B :- Pulley Block System
12 Videos
- MODERN PHYSICS -1BOOK - MOTIONCHAPTER - MODERN PHYSICS -1EXERCISE - EXERCISE-4 ( LEVEL- II)
39 Videos
- NLM & FRICTIONBOOK - MOTIONCHAPTER - NLM & FRICTIONEXERCISE - EXERCISE-4 ( LEVEL-II)
15 Videos
Similar Questions
A block of mass m is placed on a wedge of mass M. Coefficient between then is μ<cotθ. The wedge is given an acceleration to its left. Find the maximum acceleration at which block apears stationary relative to wedge.

View SolutionA block of mass m lies on wedge of mass. Mas shown in figure.

With what minimum acceleration must the wedge be moved towared right horizontally so that block m falls freely.
View Solution
Knowledge Check
A block of mass m is placed on a smooth inclined wedge ABC of inclination theta as shown in the figure. The wedge is given an acceleration a towards the right. The relation between a and theta for the block to remain stationary on the wedge is.
 Aa=gtanθBa=gcosecθCa=cosθDa=gsinθ
Aa=gtanθBa=gcosecθCa=cosθDa=gsinθA block of mass m is placed on a smooth inclined wedge ABC of inclination θ as shown in the figure. The wedge is given an acceleration 'a' towards the right. The relation between a and for the block to remain stationary on the wedge is:
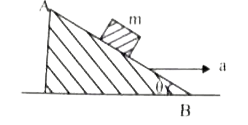 Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθ
Aa=gcosθBa=gsinθCa=gcosecθDa=gtanθA small block of mass m rests on a smooth wedge of angle θ. With what horizontal accelaration a should the wedge be pulled, as shown in fig, so that the block falls freely?
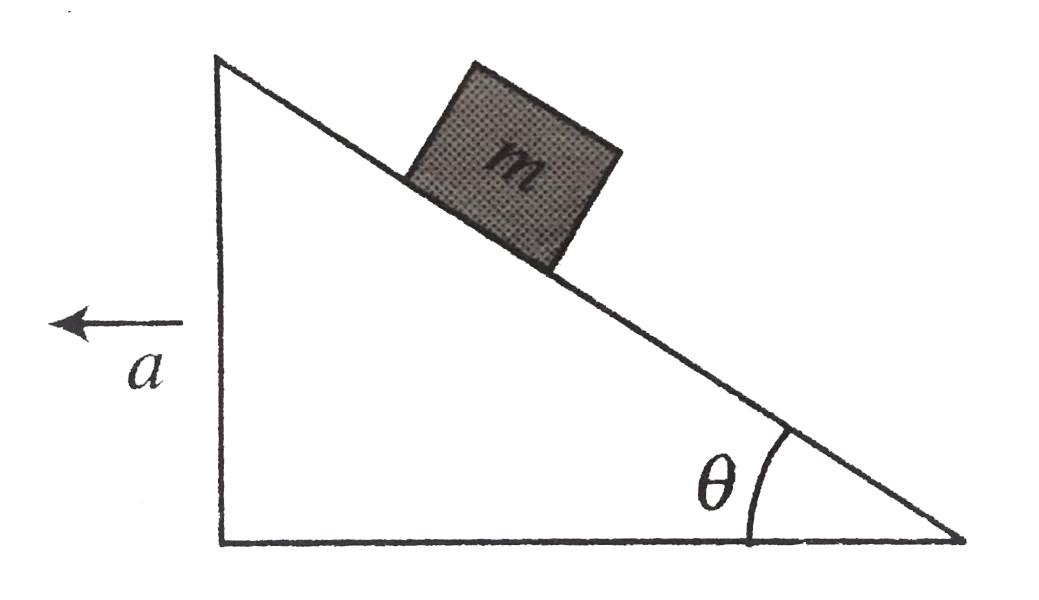 AgcosθBgsinθCgcotθDgtanθ
AgcosθBgsinθCgcotθDgtanθ
A block of mass 1.0 kg rests on a wedge of angle θ. The acceleration which should be given to the wedge so that the block falls freely is :
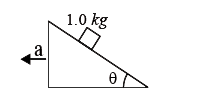
View SolutionA block of mass m, is kept on a wedge of mass M, as shown in figure such that mass m remains stationary w.r.t. wedge. The magnitude of force P is

View SolutionA block of mass m is at rest on a rought wedge as shown in figure. What is the force exerted by the wedge on the block?

View SolutionA block of mass m is lying at rest at point P of a wedge having a smooth semi-circular track of radius R. What should be the minimum value of a0 so that the mass can just reach point Q
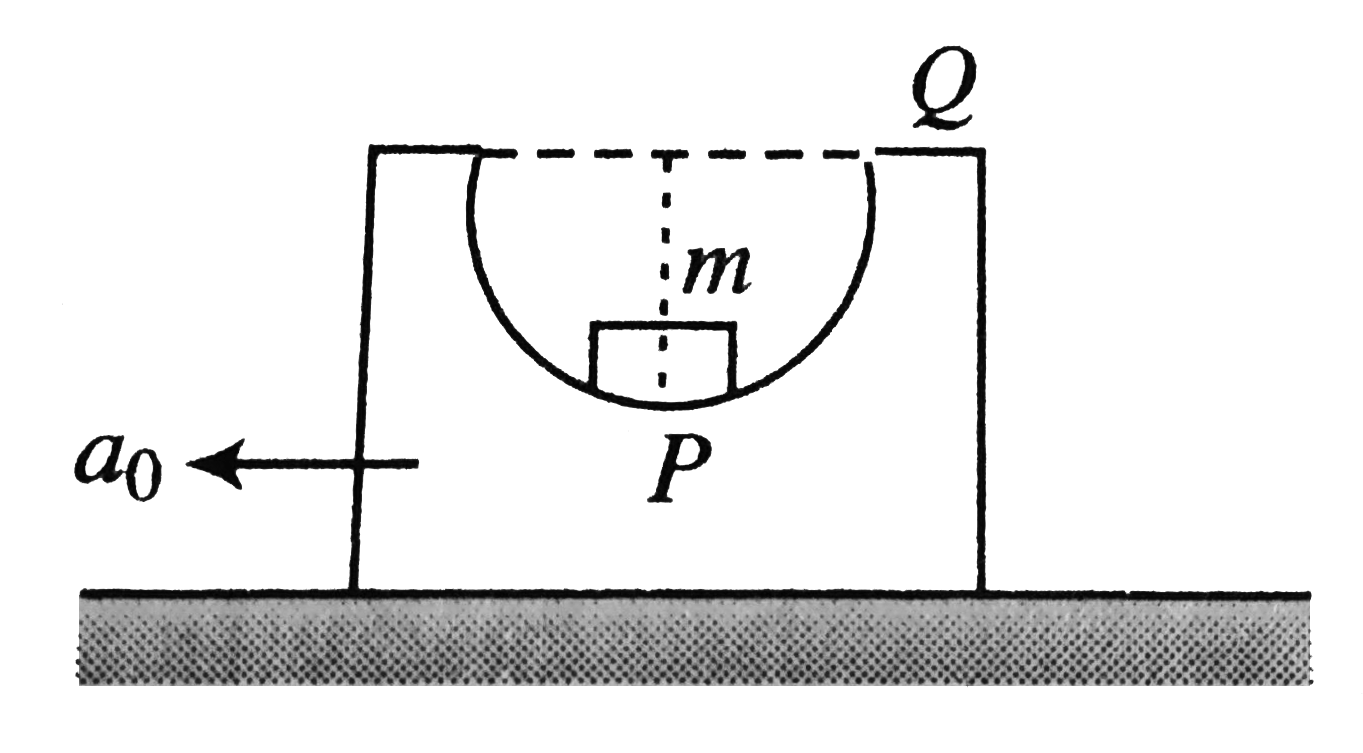
View SolutionA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?

View Solution
