The Bernoulli's equation is given by . Where P= pressure, = density, v= speed, h=height of the liquid column, g= acceleration due to gravity and k is constant. The dimensional formula for k is same as that for:
Velocity gradient
Pressure gradient
Modulus of elasticity
Thrust
Step by step video, text & image solution for The Bernoulli's equation is given by P+1/2 rho v^(2)+h rho g=k. Where P= pressure, rho= density, v= speed, h=height of the liquid column, g= acceleration due to gravity and k is constant. The dimensional formula for k is same as that for: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - UNITS AND DIMENSIONS, BASIC MATHEMATICS EXERCISE - Exercise - 3 ( Section-A Previous Year Problems )29videos
UNITS AND DIMENSIONS, BASIC MATHEMATICS
- BOOK - MOTIONCHAPTER - UNITS AND DIMENSIONS, BASIC MATHEMATICS EXERCISE - Exercise - 3 ( Section-B Previous Year Problems )10videos
UNITS AND DIMENSIONS, BASIC MATHEMATICS
- BOOK - MOTIONCHAPTER - UNITS AND DIMENSIONS, BASIC MATHEMATICS EXERCISE - Exercise - 1 (Objective Problems) (SECTION - D :- ERRORS )19videos
UNITS AND DIMENSIONS, BASIC MATHEMATICS
- BOOK - MOTIONCHAPTER - UNIT & DIMENSIONSEXERCISE - Exercise - 4 (Level - II) (PREVIOUS YEAR JEE ADVANCED)10videos
UNIT & DIMENSIONS
- BOOK - MOTIONCHAPTER - VECTOR EXERCISE - Exercise - 318videos
VECTOR
Similar Questions
Test if the following equation is dimensionally correct: h=(sScosθrpg) where h= height, S= surface tension, p= density, r=radius, and g= acceleration due to gravity.
View SolutionThe pressure at a depth h in a liquid of density d is given by pressure = __ , where g is the acceleration due to gravity.
View Solution
Knowledge Check
- Question 1 - Select One
According to Bernoulli's theorem pd+v22+gh = constant is (P is pressure, d is density, h is height, v is velocity and g is acceleration due to gravity)
A[M0L0T0]B[M0LT0]C[M0L2T−2]D[M0L2T−4] - Question 2 - Select One
Given as : h=2Scosθrρg where S is the surface tension of liquid, r is the radius of capillary tube. ρ is the density and g is acceleration due to gravity then dimensional formula for S is:
A[ML0T−2]B[M0LT−2]C[ML2T−2]D[M0L0T−3] - Question 3 - Select One
The height of liquid column in capillary tube is h the radius of capillary tube is r.ρ is the density of liquid , g is acceleration due to gravity and θ is angle of contact . The surface tension of the liquid is ,
At=rhρg2cosθBT=2cosθhρgrCT=2cosθrρhgDall of these
Check by the method of dimensions, whether the folllowing relation are dimensionally correct or not. (i) υ=√P/ρ, where υ is velocity. P is prerssure and ρ is density. (ii) v=2π√Ig, where I is length, g is acceleration due to gravity and v is frequency.
View SolutionA formula is given as P=ba√1+k.θ.t3m.a
where P = pressure, k = Boltzmann's constant,
θ= temperature, t= time, 'a' and 'b' are constants.
Dimensional formula of 'b' is same asView SolutionA storage tower supplies water, as shown in the figure. If P0 is the atmospheric pressure h = height of water level, g = acceleration due to gravity, ρ= density and v = velocity of flow in the horizontal pipe at B, then the pressure at B is -
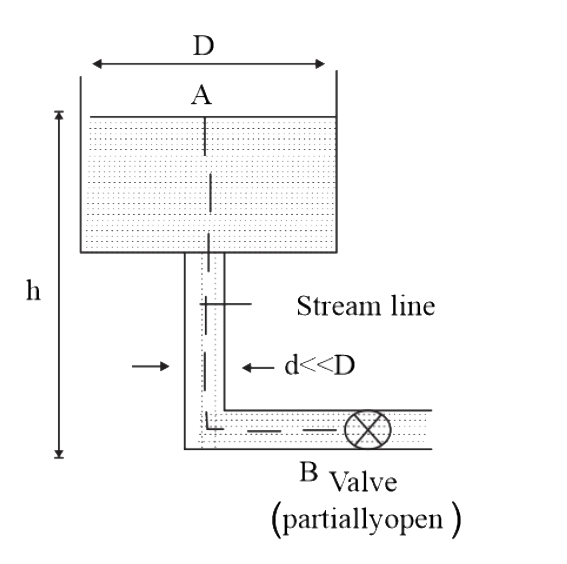 View Solution
View SolutionA liquid drop placed on a horizontal plane has a near spherical shape (slightly flattened due to gravity). Let R be the radius of its largest horizontal section. A small disturbance causes the drop to vibrate with frequency v about its equilibrium shape. By dimensional analysis the ratio v√σ/ρR3 can be (Here σ is surface tension, ρ is density, g is acceleration due to gravity, and k is arbitrary dimensionless constant)–
View SolutionThe absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
View Solution

