A conducting rod rotates with a constant angular velocity $' ω'$ about the axis which passes through point 'O' and perpendicular to its length . A uniform magnetic field 'B' exists parallel to the axis of the rotation . Then potential difference between the two ends of the rod is :-

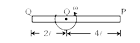
$6 B ω l^{2}$

$B ω l^{2}$

$10 B ω l^{2}$

Zero

Video Solution

Text Solution

Verified by Experts

The correct Answer is:a

Updated on:21/07/2023

Answer

Step by step video, text & image solution for A conducting rod rotates with a constant angular velocity 'omega' about the axis which passes through point 'O' and perpendicular to its length . A uniform magnetic field 'B' exists parallel to the axis of the rotation . Then potential difference between the two ends of the rod is :- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Knowledge Check

A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is
A $\frac{B l^{2} ω}{2}$
Bzero
C $(\frac{B l^{2} ω}{8})$
D $2 B l^{2} ω$
A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is
Azero
B $\frac{1}{2} ω B I^{2}$
C $ω B I^{2}$
D $2 ω B I^{2}$
A rod of length l is rotated with angular speed $ω$ about an axis passing through the centre of rod and perpendicular to its length. A uniform magnetic field B is applied parallel to the axis of rotation, Potential difference developed between the ends of the rod is
A $B l \frac{ω^{2}}{2}$
B $B l (ω^{2})$
C $B l \frac{ω^{2}}{8}$
DZero

MOTION-ELECTRO MAGNETIC INDUCTION-EXERCISE-2 (Objective problems (Analytical questions))

Home
Ask Doubt
Profile

A conducting rod rotates with a constant angular velocity 'ω' about the axis which passes through point 'O' and perpendicular to its length . A uniform magnetic field 'B' exists parallel to the axis of the rotation . Then potential difference between the two ends of the rod is :-

The correct Answer is:a

Topper's Solved these Questions

Similar Questions

Knowledge Check

A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is

A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is

A rod of length l is rotated with angular speed ω about an axis passing through the centre of rod and perpendicular to its length. A uniform magnetic field B is applied parallel to the axis of rotation, Potential difference developed between the ends of the rod is

MOTION-ELECTRO MAGNETIC INDUCTION-EXERCISE-2 (Objective problems (Analytical questions))

A conducting rod rotates with a constant angular velocity $' ω'$ about the axis which passes through point 'O' and perpendicular to its length . A uniform magnetic field 'B' exists parallel to the axis of the rotation . Then potential difference between the two ends of the rod is :-

A rod of length l is rotated with angular speed $ω$ about an axis passing through the centre of rod and perpendicular to its length. A uniform magnetic field B is applied parallel to the axis of rotation, Potential difference developed between the ends of the rod is