The armature coil of dynamo is in motion . The generated induced emf varies and the number of magnetic lines of force also varies . Which of the following condition is correct :-
lines of flux will be minimum, but induced emf will be zero
lines of flux will be maximum, but the induced emf will be zero
line of flux will be maximum, but induced emf will be not be zero .
the lines of flux will be maximum, and the induced emf will be also maximum.
The correct Answer is:b
To solve the problem regarding the conditions of induced EMF and magnetic flux in the armature coil of a dynamo, we can follow these steps:
1. Understanding the Setup:
- The armature coil of a dynamo is rotating in a magnetic field. The magnetic field lines and the area vector of the coil determine the magnetic flux through the coil.
2. Magnetic Flux Calculation:
- The magnetic flux (Φ) through the coil is given by the formula:
Φ=B⋅A⋅cos(θ)
where B is the magnetic field strength, A is the area of the coil, and θ is the angle between the magnetic field and the normal to the surface of the coil.
3. Rotation of the Coil:
- As the coil rotates, the angle θ changes. If the coil is rotated with a uniform angular velocity ω, then θ can be expressed as:
θ=ωt
- Thus, the magnetic flux can be rewritten as:
Φ(t)=B⋅A⋅cos(ωt)
4. Induced EMF Calculation:
- The induced EMF (E) in the coil can be calculated using Faraday's law of electromagnetic induction:
E=−ndΦdt
where n is the number of turns in the coil.
5. Differentiating the Flux:
- To find the induced EMF, we differentiate the magnetic flux:
dΦdt=−B⋅A⋅ωsin(ωt)
- Therefore, the induced EMF becomes:
E=nBAωsin(ωt)
6. Analyzing Conditions:
- The induced EMF is a function of sin(ωt), which means it will be zero when ωt is an integer multiple of π (0, π, 2π, ...).
- The magnetic flux, however, is at its maximum when cos(ωt) is at its maximum (1 or -1), which occurs at the same points.
7. Conclusion:
- Therefore, when the magnetic flux is maximum, the induced EMF is zero. This leads us to conclude that the correct condition is:
- "Lines of flux will be maximum but induced EMF will be zero."
Final Answer:
The correct condition is: Lines of flux will be maximum but induced EMF will be zero.
---
- The armature coil of a dynamo is rotating in a magnetic field. The magnetic field lines and the area vector of the coil determine the magnetic flux through the coil.
- The magnetic flux (Φ) through the coil is given by the formula:
Φ=B⋅A⋅cos(θ)
where B is the magnetic field strength, A is the area of the coil, and θ is the angle between the magnetic field and the normal to the surface of the coil.
- As the coil rotates, the angle θ changes. If the coil is rotated with a uniform angular velocity ω, then θ can be expressed as:
θ=ωt
- Thus, the magnetic flux can be rewritten as:
Φ(t)=B⋅A⋅cos(ωt)
- The induced EMF (E) in the coil can be calculated using Faraday's law of electromagnetic induction:
E=−ndΦdt
where n is the number of turns in the coil.
- To find the induced EMF, we differentiate the magnetic flux:
dΦdt=−B⋅A⋅ωsin(ωt)
- Therefore, the induced EMF becomes:
E=nBAωsin(ωt)
- The induced EMF is a function of sin(ωt), which means it will be zero when ωt is an integer multiple of π (0, π, 2π, ...).
- The magnetic flux, however, is at its maximum when cos(ωt) is at its maximum (1 or -1), which occurs at the same points.
- Therefore, when the magnetic flux is maximum, the induced EMF is zero. This leads us to conclude that the correct condition is:
- "Lines of flux will be maximum but induced EMF will be zero."
The correct condition is: Lines of flux will be maximum but induced EMF will be zero.
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - EXERCISE-3 (Assertion & Reasoning)18videos
ELECTRO MAGNETIC INDUCTION
- BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - EXERCISE-4| Section A (Prevous Years Problems )28videos
ELECTRO MAGNETIC INDUCTION
- BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - EXERCISE-172videos
ELECTRO MAGNETIC INDUCTION
- BOOK - MOTIONCHAPTER - Electrical Instrument EXERCISE - EXERCISE -316videos
Electrical Instrument
- BOOK - MOTIONCHAPTER - ELECTRO MAGNETIC WAVES EXERCISE - EXERCISE - 3 (SECTION - B)8videos
ELECTRO MAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
The coil of dynamo is rotating in a magnetic field. The developed induced e.m.f. changes and the number of magnetic lines of force also changes. Which of the following condition is correct
ALines of force minimum but induced e.m.f. is zeroBLines of force maximum but induced e.m.f. is zeroCLines of force maximum but induced e.m.f. is not zeroDLines of force maximum but induced e.m.f. is also maximum - Question 2 - Select One
Which of the following is a correct representation of magnetic lines of force?
A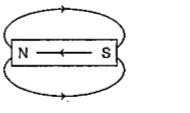 B
B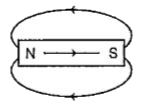 C
C Dnone of the above
Dnone of the above - Question 3 - Select One
A magnet and a coil are taken. In which of the following cases, emf is induced in the coil ?
Amagnet is moving, coil is at rest.Bmagnet is at rest and the coil is moving.Cboth magnetic and coil are moving with equal velocities.Dmagnet is moving with greater velocity than that of coil.
Which of the followfng statements is wrong? Magnetic lines of force
View SolutionThe current i in an induction coil varies with time according to the graph shown in figure. Which of the following graph shows induced emf in the coil with time:
View SolutionA magnet is in form of a bar as shown in the figure. The line joining the center of the bar and the center of the coil (central axis) is perpendicular to the plane of the oil. Which of the following motions of the bar will not induce electric current in the coil?
View SolutionCurrent through the coil varies according to graph then induced emf v/s time graph is
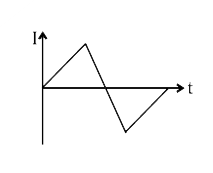 View Solution
View SolutionThe variation of magnetic field (B) due to circular coil as the distance X varies is shown in the graph. Which of the following is false
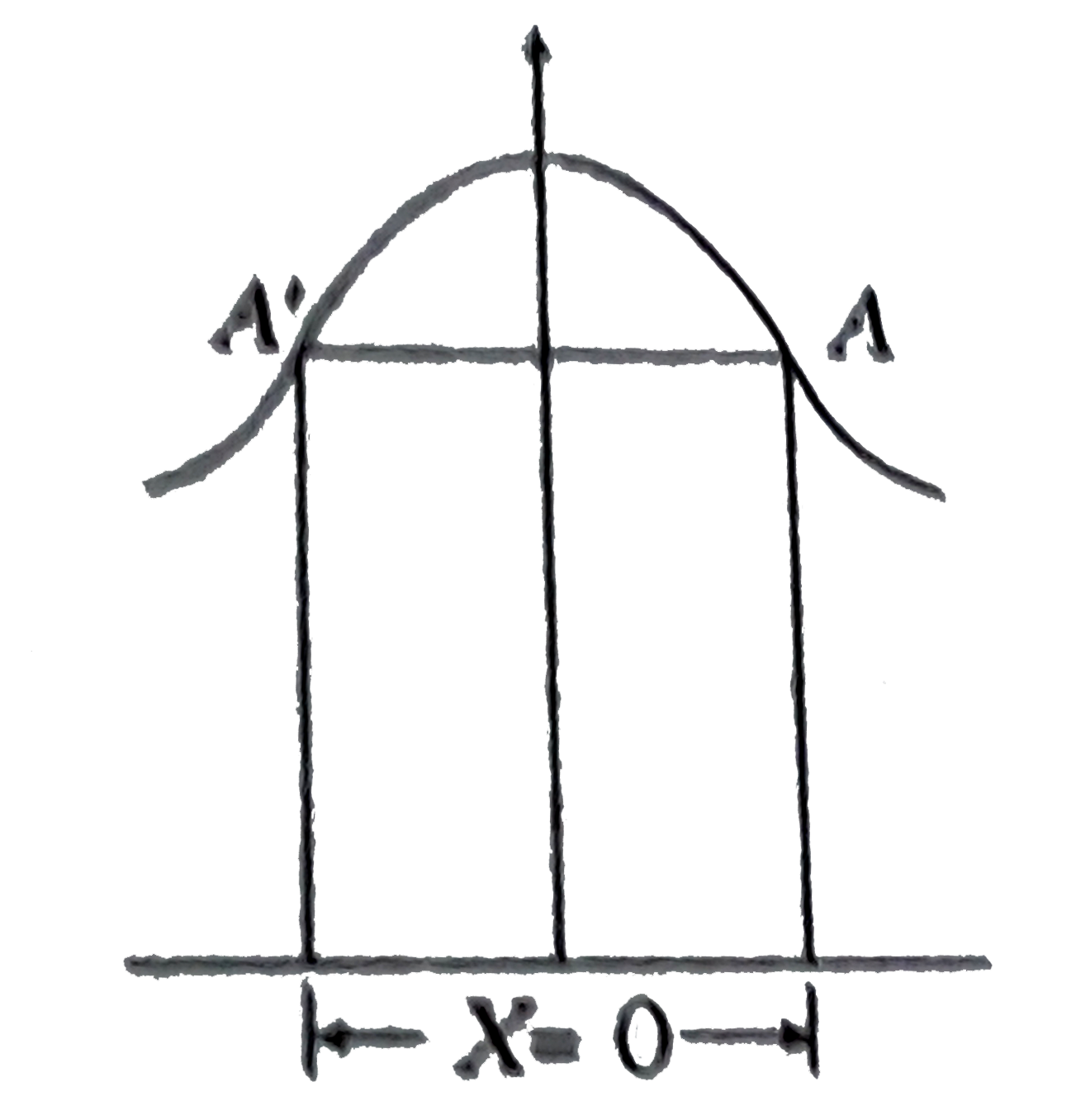 View Solution
View Solution

