A C. R series circuit is connected to a battery of e.m.f E. The time required by the capacitor to acquire maximum charge, depends upon -
R only
C only
RC
applied potential difference
The correct Answer is:C
To solve the problem of how the time required for a capacitor to acquire maximum charge in a C-R series circuit depends on certain factors, we can follow these steps:
1. Understanding the Circuit:
- We have a capacitor (C) and a resistor (R) in series connected to a battery with an electromotive force (e.m.f) E. Initially, the capacitor is uncharged.
2. Applying Kirchhoff's Voltage Law (KVL):
- According to KVL, the sum of the potential differences in a closed loop is equal to zero. For our circuit, we can write:
E−QC−I⋅R=0
- Here, Q is the charge on the capacitor at time t, and I is the current flowing through the circuit.
3. Relating Current and Charge:
- The current I can be expressed in terms of the charge Q:
I=dQdt
- Substituting this into the KVL equation gives:
E−QC−RdQdt=0
4. Rearranging the Equation:
- Rearranging the equation, we get:
dQdt=E−QCR
5. Separating Variables:
- We can separate variables to integrate:
dQE−QC=dtR
6. Integrating Both Sides:
- Integrate the left side from 0 to Q and the right side from 0 to t:
∫Q0dQE−QC=∫t0dtR
7. Calculating the Integral:
- The left side integral results in:
−Cln(E−QC)∣∣∣Q0=tR
- This leads to:
−C(ln(E−QC)−ln(E))=tR
8. Finding Maximum Charge:
- The maximum charge Q0 on the capacitor is given by:
Q0=CE
- As t approaches infinity, the capacitor will charge towards Q0.
9. Determining Time for Practical Charging:
- For practical purposes, we consider the capacitor to be fully charged when it reaches about 98% of Q0:
Q≈0.98Q0
- From the earlier equations, we can derive the time t required to reach this charge.
10. Final Conclusion:
- The time required for the capacitor to charge significantly depends on both the resistance R and the capacitance C. Thus, we conclude that the time taken by the capacitor to acquire maximum charge depends on the product RC.
- We have a capacitor (C) and a resistor (R) in series connected to a battery with an electromotive force (e.m.f) E. Initially, the capacitor is uncharged.
- According to KVL, the sum of the potential differences in a closed loop is equal to zero. For our circuit, we can write:
E−QC−I⋅R=0
- Here, Q is the charge on the capacitor at time t, and I is the current flowing through the circuit.
- The current I can be expressed in terms of the charge Q:
I=dQdt
- Substituting this into the KVL equation gives:
E−QC−RdQdt=0
- Rearranging the equation, we get:
dQdt=E−QCR
- We can separate variables to integrate:
dQE−QC=dtR
- Integrate the left side from 0 to Q and the right side from 0 to t:
∫Q0dQE−QC=∫t0dtR
- The left side integral results in:
−Cln(E−QC)∣∣∣Q0=tR
- This leads to:
−C(ln(E−QC)−ln(E))=tR
- The maximum charge Q0 on the capacitor is given by:
Q0=CE
- As t approaches infinity, the capacitor will charge towards Q0.
- For practical purposes, we consider the capacitor to be fully charged when it reaches about 98% of Q0:
Q≈0.98Q0
- From the earlier equations, we can derive the time t required to reach this charge.
- The time required for the capacitor to charge significantly depends on both the resistance R and the capacitance C. Thus, we conclude that the time taken by the capacitor to acquire maximum charge depends on the product RC.
Topper's Solved these Questions
Similar Questions
An air capacitor C connected to a battery of e.m.f. V acquires a charge q and energy E. The capacitor is disconnected from the battery and a dielectric slab is placed between the plates. Which of the following statements is correct ?
View SolutionA capacitor having capacitance 'C' is charged by a battery having e.m.f. 2V (Battery is disconnected after charging). Now this charged capacitor is connected to another battery having e.m.f. V. The positive plate of capacitor is connected with -ve terminal of battery & vice-versa. The amount of heat produced after connecting it with battery. +q
View Solution
Knowledge Check
An L-C-R series circuit , connected to a source E, is at resonance. Then,
Athe voltage across R is zeroBthe voltage across R equals applied voltageCthe volatage across C is zeroDthe voltage across C equals applied voltageAn external resistance R is connected to a battery of e.m.f. V and internal resistance r . The joule heat produced in resistor R is maximum when R is equal to
ArBr2C2rDInfinitely largeTwo capacitors C1=3μF and C2=6μF in series, are connected in parallel to a third capacitor C3=4μF. This arrangement is then connected to a battery of e.m.f., =30V, as shown. The energy lost by the battery in charging the capacitors
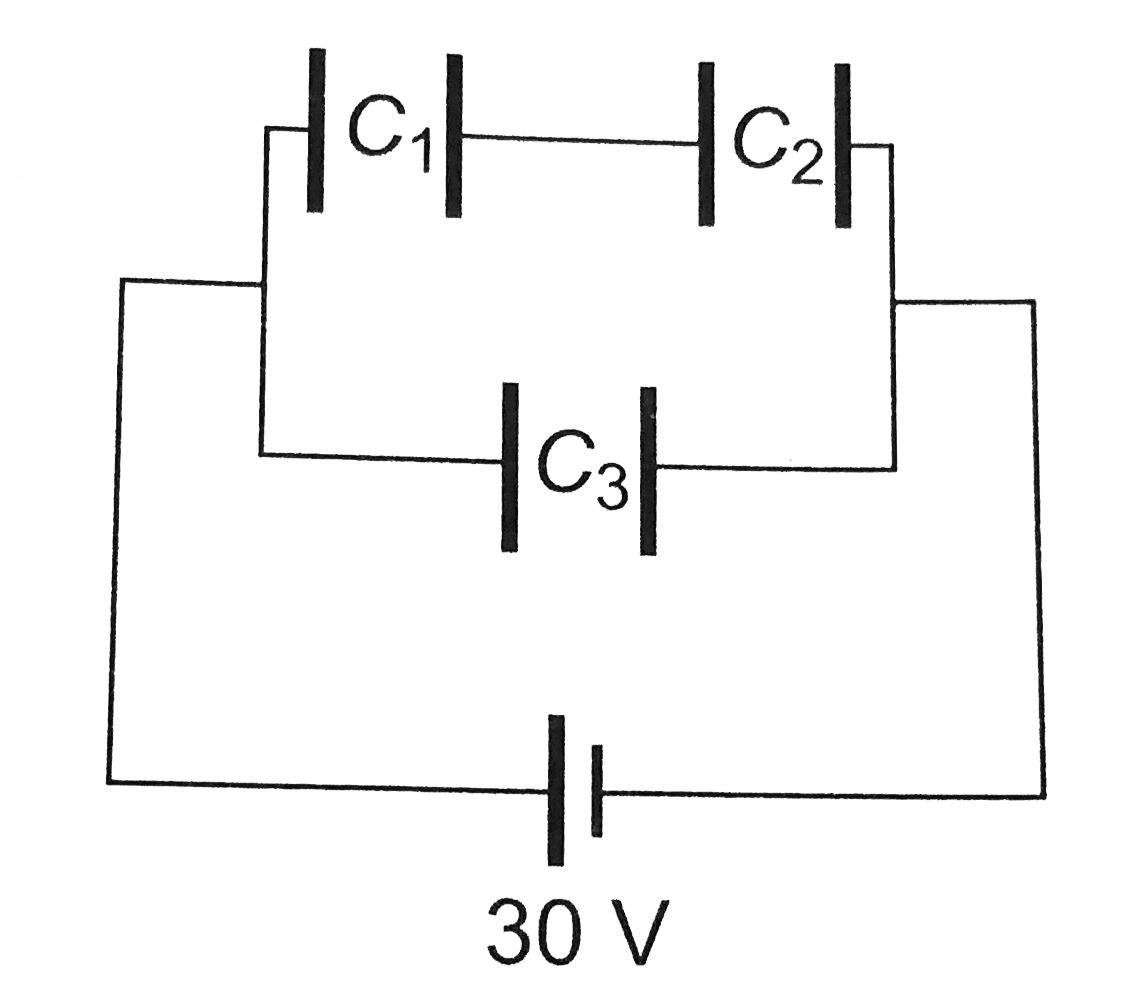 A900μJB1800μJC2700μJD3600μJ
A900μJB1800μJC2700μJD3600μJ
A capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance 10(μ)F is connected to a battery of emf 2V.It is found that it takes 50 ms for the charge on the capacitor to bacome 12.6(μ)C.find the resistance of the circuit.
View SolutionA series combination of three capacitors of capacities 1μF,2μF and 8μF is connected to a battery of e.m.f. 13vo<. The potential difference across the plates of 2μF capacitor will be
View SolutionA series combination of L and R is connected to a battery of emf E having negligible internal resistance. The final value of current depeds upon
View SolutionFigure shows a LCR circuit connected with a battery emf ε and internal resistance 'R'. After a long time (initially the capacitor was uncharged)

View Solution
