A closed cubical box made of a perfectly insulating material has walls of thickness 8 cm and the only way for the heat to enter or leave the box is through two solid cylinderical metal plugs , each of cross - sectional area $12 c m^{2}$ and length 8 cm fixed in the opposite walls of the box . The outer surface A of one plug is kept at a temperature of $100^{\circ} C$ while the outer surface of the other plug is maintained at a temperature of $4^{\circ} C ~ . T h e t h e r m a l c o \in d u c t i v i t y o f t h e m a t e r i a l o f t h e p l u g i s$ 0.5 cal // cmsec""^(@)C $. A s o u r c e o f e \neq r g y \geq \neq r a t \in g$ 36 cal s^(-1) is enclosed inside the box . Find the equilibrium temperature of the inner surface of the box assuming that it is the same at all points on the inner surface

Text Solution

Verified by Experts

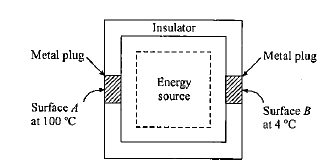
At equilibrium, the total energy generated by the source per second is equal to the heat leaving per second through the two metal plugs (Figure-4.12). Let T°C be the equilibrium temperature. Then heat leaving the box per second through surface A
$\frac{k (T - 100) \times 12}{8} c a l s^{- 1}$
Heat leaving the box per second through the surface B
$\frac{k (T - 4) \times 12}{8} c a l s^{- 1}$
Hence $\frac{12 k}{8} (T - 100 + T - 4) = 36$
or $2 T - 104 = \frac{36 \times 8}{12 k} = \frac{36 \times 8}{12 \times 0.5} = 48 or T = 76^{\circ} C$

Updated on:21/07/2023