A block having some emissivity is maintained at 500 K temperature in a surrounding of300 K temperature. It isobserved that, to maintain the temperature of the block, 210 W external power is required to be supplied to it. If instead ofthis block a black body ofsame geometry and size is used, 700 W external power is needed for the same. Find the emissivity of the material ofthe block.
To find the emissivity of the block, we can use Stefan-Boltzmann's law, which relates the power radiated by a body to its temperature and emissivity. The formula for power loss due to radiation is given by:
P=σ⋅e⋅A⋅(T4−T4s)
Where:
- P is the power radiated,
- σ is the Stefan-Boltzmann constant (5.67×10−8W/m2K4),
- e is the emissivity of the body,
- A is the surface area of the body,
- T is the absolute temperature of the body,
- Ts is the absolute temperature of the surroundings.
1. Identify the given values:
- Temperature of the block, T=500K
- Temperature of the surroundings, Ts=300K
- Power required to maintain the temperature of the block, P1=210W
- Power required to maintain the temperature of a black body, P2=700W
2. Set up the equations for power loss:
- For the block with emissivity e:
P1=σ⋅e⋅A⋅(T4−T4s)
- For the black body (where e=1):
P2=σ⋅1⋅A⋅(T4−T4s)
3. Express the equations:
- From the first equation:
210=σ⋅e⋅A⋅(5004−3004)
- From the second equation:
700=σ⋅A⋅(5004−3004)
4. Divide the two equations:
P1P2=σ⋅e⋅A⋅(5004−3004)σ⋅A⋅(5004−3004)
This simplifies to:
210700=e
5. Calculate the emissivity:
e=210700=0.3
Final Answer:
The emissivity of the material of the block is e=0.3.
- P is the power radiated,
- σ is the Stefan-Boltzmann constant (5.67×10−8W/m2K4),
- e is the emissivity of the body,
- A is the surface area of the body,
- T is the absolute temperature of the body,
- Ts is the absolute temperature of the surroundings.
- Temperature of the block, T=500K
- Temperature of the surroundings, Ts=300K
- Power required to maintain the temperature of the block, P1=210W
- Power required to maintain the temperature of a black body, P2=700W
- For the block with emissivity e:
P1=σ⋅e⋅A⋅(T4−T4s)
- For the black body (where e=1):
P2=σ⋅1⋅A⋅(T4−T4s)
- From the first equation:
210=σ⋅e⋅A⋅(5004−3004)
- From the second equation:
700=σ⋅A⋅(5004−3004)
P1P2=σ⋅e⋅A⋅(5004−3004)σ⋅A⋅(5004−3004)
This simplifies to:
210700=e
e=210700=0.3
The emissivity of the material of the block is e=0.3.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Practice Exercise 4.35videos
HEAT TRANSFER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Practice Exercise 4.45videos
HEAT TRANSFER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Practice Exercise 4.111videos
HEAT TRANSFER
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO82videos
HEAT AND THERMAL EXPANSION
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO64videos
Kinetic Theory of Gases and Gas Laws
Similar Questions
A spherical ball of radius 1cm coated with a metal having emissivity 0.3 is maintained at 1000 K temperature and suspended in a vacuum chamber whose walls are maintained at 300 K temperature. Find rate at which electrical energy is to be supplied to the ball to keep its temperature constant.
View SolutionA spherical metal ball of radius 1 cm is suspended in a room at 300 K temperature. Inside the sphere there is a battery operated heater which maintains the temperature of the ball at 1000 K. Find the power of the heater if emissivity of the metal ball is 0.3.
View Solution
Knowledge Check
- Question 1 - Select One
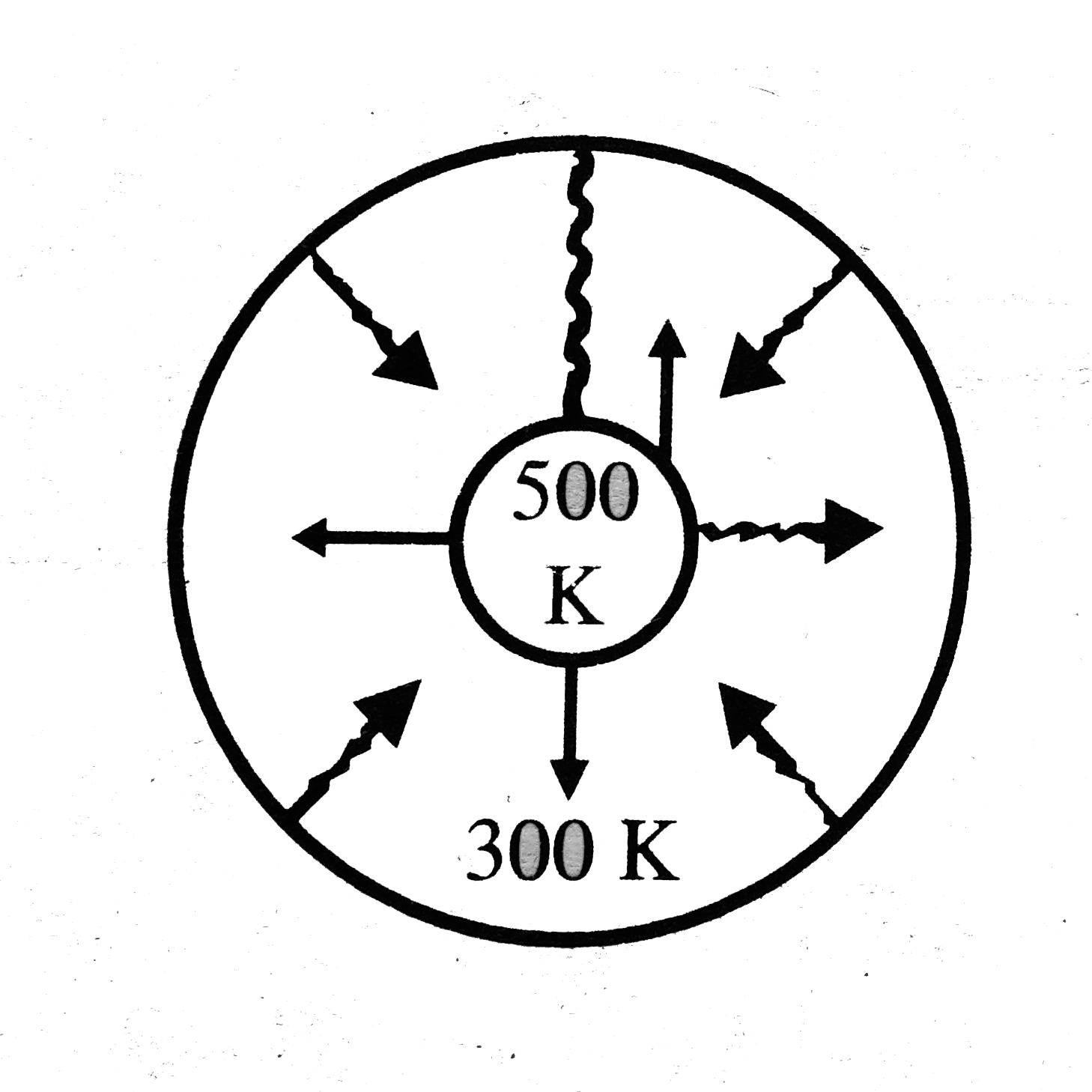
A copper sphere is suspended in an evacuated chamber maintained at 300 K. The sphere is maintained at a constant temperature of 500 K by heating it electrically. A total of 210 W of electric power is needed to do it. When the surface of the copper sphere is completely blackened, 700 W is needed to maintain the same temperature of the sphere. Calculate the emissivity of copper.A0.3B0.2C0.5DNone of these - Question 2 - Select One
A spherical black body with a radius of 12cm radiates 450W power at 500K. If the radius were halved and the temperature doubled, the power radiated in watt would be
A225B450C900D1800 - Question 3 - Select One
A spherical black body with a radius of 20 cm radiates 440 W power at 500 K. If the radius were halved and the temperature doubled, the power radiated in watt would be
A225B450C980D1760
A copper sphere is suspended in an evacuated chamber maintained at 300K. The sphere is maintained at a constant temperature of 500K by heating it electrically. A total of 210W is electric power is needed to do it. When the surface of the copper sphere is completely blanked, 700W is needed to maintain the same temperature of the sphere. Calculate the emissivity of copper.
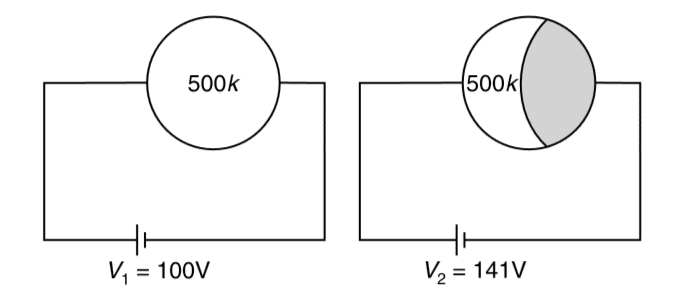
View SolutionA copper sphere is maintained at 500 K temperature by connecting it to a battery of emf V1=100 V (see figure). The surrounding temperature is 300 K. When half the surface of the copper sphere is completely blackened (so that the surface behaves almost like a black body), a cell of emf V2 = 141 V is needed to maintain its temperature at 500 K. Calculate the emissivity of the copper surface.
 View Solution
View SolutionA copper sphere is suspended in an evacuated chamber maintained at 300K. The sphere is mantained at a constant temperature of 500K by heating it electrically. A total of 300W of electric power is needed to do it. When half of the surface of the copper sphere is completely blackened, 600W is needed to maintain the same temperature of the the sphere. Calculate the emissivity of copper.
View SolutionA spherical black body with radius 12 cm radiates 450 W power at 500 K. If the radius is halved and temperature is doubled, the power radiated in watt would be
View SolutionA metal block is placed in a room which is at 10∘C. It is heated by an electric heater of power 500W till its temperature becomes 50∘C. Its initial rate of rise of temperature is 2.5∘C/sec. The heater is switched off and now a heater of 100W is required to maintain the temperature of the block at 50∘C. (Assume Newtons Law of cooling to be valid)
(i) What is the heat capacity of the block ?
(ii) What is the rate of cooling of block at 50∘C if the 100W heater is also switched off ?
(iii) What is the heat radiated per second when the block was 30∘C ?View Solution

