Two cylindrical rods of lengths l1 and l2, radii r1 and r2 have thermal conductivities k1 and k2 respectively. The ends of the rods are maintained at the same temperature difference. If l1=2l2 and r1=r2/2, the rates of heat flow in them will be the same if k1/k2 is:
1
2
4
8
The correct Answer is:D
To solve the problem, we need to find the ratio of thermal conductivities k1k2 for two cylindrical rods under the given conditions. Let's go through the solution step by step.
Step 1: Understand the Heat Flow Formula
The rate of heat flow dQdt through a cylindrical rod is given by the formula:
dQdt=kA(T1−T2)L
where:
- k is the thermal conductivity,
- A is the cross-sectional area,
- T1−T2 is the temperature difference across the ends of the rod,
- L is the length of the rod.
Step 2: Define the Areas of the Cylindrical Rods
For a cylindrical rod, the cross-sectional area A is given by:
A=πr2
where r is the radius of the rod.
Step 3: Set Up the Equations for Both Rods
Let’s denote the parameters for the two rods:
- For rod 1: l1=2l2, r1=r22
- For rod 2: l2, r2
The areas for the rods are:
- A1=πr21=π(r22)2=πr224
- A2=πr22
Step 4: Write the Heat Flow Equations
For rod 1:
dQ1dt=k1A1(T1−T2)l1=k1(πr224)(T1−T2)2l2
For rod 2:
dQ2dt=k2A2(T1−T2)l2=k2πr22(T1−T2)l2
Step 5: Set the Heat Flow Rates Equal
Since the rates of heat flow are the same:
k1(πr224)(T1−T2)2l2=k2πr22(T1−T2)l2
Step 6: Cancel Common Terms
We can cancel πr22(T1−T2) and l2 from both sides:
k12=k2
Step 7: Express k1k2
Rearranging gives:
k1=2k2
Thus,
k1k2=2
Step 8: Substitute the Radius Relation
Now, substituting the radius relation r1=r22:
k1k2=⎛⎝r2r22⎞⎠2⋅2=(2)2⋅2=4⋅2=8
Final Result
Thus, the ratio of thermal conductivities is:
k1k2=8
The rate of heat flow dQdt through a cylindrical rod is given by the formula:
dQdt=kA(T1−T2)L
where:
- k is the thermal conductivity,
- A is the cross-sectional area,
- T1−T2 is the temperature difference across the ends of the rod,
- L is the length of the rod.
For a cylindrical rod, the cross-sectional area A is given by:
A=πr2
where r is the radius of the rod.
Let’s denote the parameters for the two rods:
- For rod 1: l1=2l2, r1=r22
- For rod 2: l2, r2
- A1=πr21=π(r22)2=πr224
- A2=πr22
For rod 1:
dQ1dt=k1A1(T1−T2)l1=k1(πr224)(T1−T2)2l2
For rod 2:
dQ2dt=k2A2(T1−T2)l2=k2πr22(T1−T2)l2
Since the rates of heat flow are the same:
k1(πr224)(T1−T2)2l2=k2πr22(T1−T2)l2
We can cancel πr22(T1−T2) and l2 from both sides:
k12=k2
Rearranging gives:
k1=2k2
Thus,
k1k2=2
Now, substituting the radius relation r1=r22:
k1k2=⎛⎝r2r22⎞⎠2⋅2=(2)2⋅2=4⋅2=8
Thus, the ratio of thermal conductivities is:
k1k2=8
Topper's Solved these Questions
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Advance MCQs with One or More Option Correct
20 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO
66 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Conceptual MCQs Single Option Correct
24 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
Similar Questions
Consider two rods of equal cross - sectionai area A, one of Aluminium and other of iron joined end to end as shown in figure -4.8. Length of the two rods and their thermal coductivities are l1,k1and l2,k2 respectively . If the ends of the rods are maintained at temperature T1 and T2,(T1>T2) find the temperature of the junction in steady state .

View SolutionTwo walls of thicknes l1 and l2 and ther-mal condctivities K1 and K2 are in contact In the steady state, if the temperature at the outer faces are T1 and T2 find the temperature at the common wall .
View Solution
Knowledge Check
Two rods of length l1 and l2 are made of material whose coefficient of linear expansion are α1 and α2 , respectively. The difference between their lengths will be independent of temperatiure if l1/l2 is to
Aα1α2Bα2α1C(α1α2)1/2D(α2α1)1/2Two rods of length d1 and d2 and coefficients of thermal conductivites K1 and K2 are kept touching each other. Both have the same area of cross-section. The equivalent thermal conductivity.
AK1+K2BK1d1+K2d2CK2d1+K1d2d1+d2Dd1+d2d1K1+d2K2Two rods one is semi circular of thermal conductivity K1 and otheir is straight of thermal conductivity K2 and of same cross sectional area are joined as shown in the The points A and B are maintained at same temperature difference. If rate of flow of heat is same in two rods then K1/K2 is
 .A2:πB1:2Cπ:2D3:2
.A2:πB1:2Cπ:2D3:2
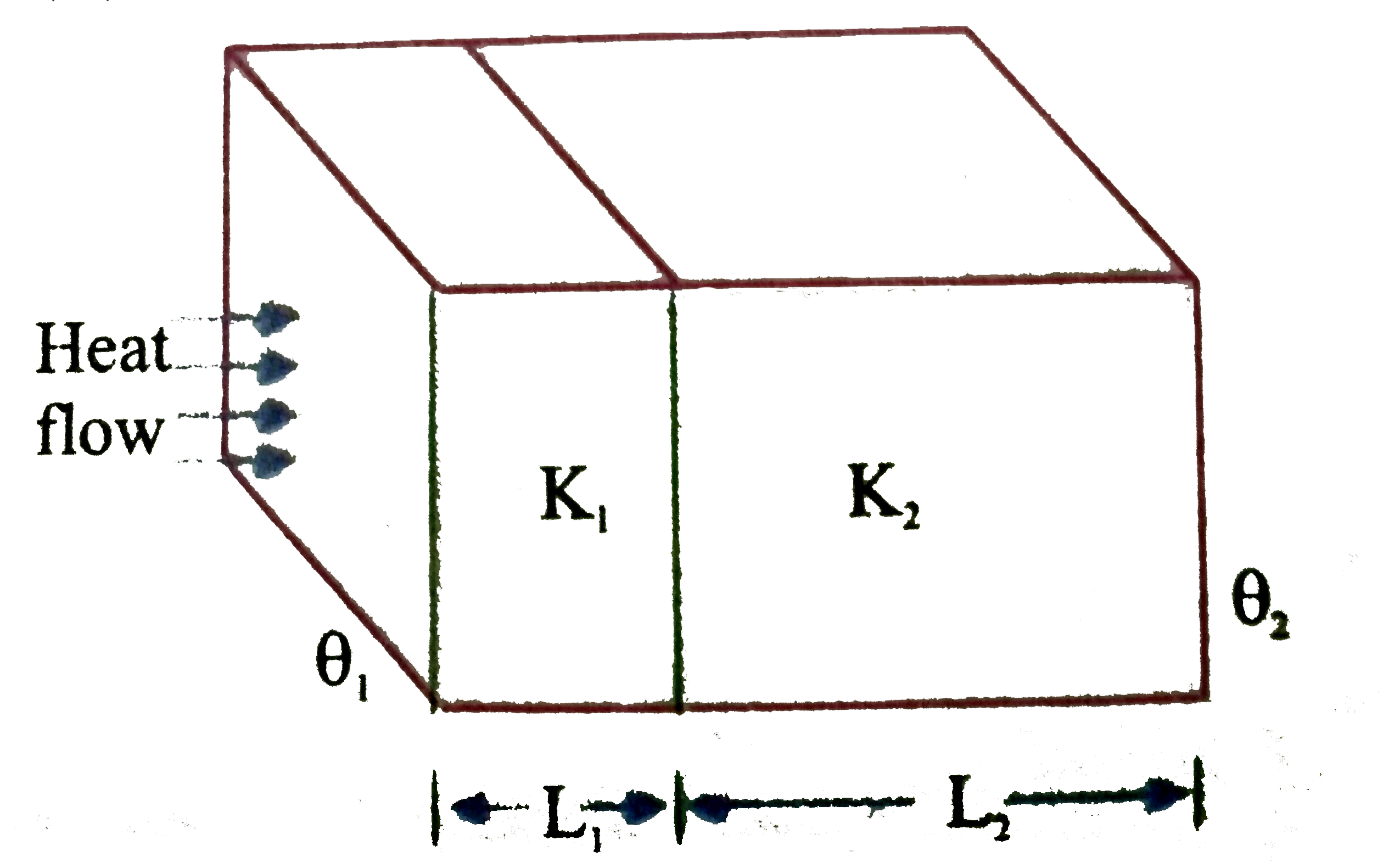
Two plates each of area A thickness L1 and L2 thermal conductivities K1 and K2 respectively are joined to from a single plate of thickness (L1+L2) If the temperatures of the free surfaces are θ1 and θ2 Calculate
(a) Rate of flow of heat
(b) Temperature of interface
 .
.
View SolutionTwo rods of the same length and diameter, having thermal conductivities K1 and K2, are joined in parallel. The equivalent thermal conductivity to the combinationk is
View SolutionTwo rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
View SolutionTwo rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
View SolutionRate of heat flow through two conducting rods of identiclal dimensions having thermal conductivities K1 and K2 and Q1 and Q2 when their ends are maintained at the same difference of temperature individually. When the two rods are joined in series with their ends maintained at the same temperature difference (as shown in the figure), the rate of heat flow will be

View Solution
