l-neural system, 2-endocrine, 3-hormones, 4-neurons

A force $\to F = 5 \to i + 2 \to j + \to k$ displaces a body from a point with coordinates (1,1,1) to another point with coordinates (2,0,3).Calculate the work done by the force.All are in SI units.

View Solution

Early crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii.
Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller catin fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
$\begin{matrix} Coordiantion number & Geometry & ρ = \frac{r_{cation}}{r_{amion}} 2 & linear & 0 - 0.155 3 & triangular & 0.155 - 0.225 4 & tetrahedral & 0.225 - 0.414 4 & square planar & 0.414 - 0.732 6 & octahedral & 0.414 - 0.732 8 & cubic & 0.732 - 1.0 12 & cuboctahedral & 1.0 \end{matrix}$
(Source : Ionic Radii and Radius Ratios. (2021, June 8). Retrieved June 29, 2021, from https://chem.ibretexts.org/@go/page/183346)
The radius of $A g^{+}$ ion is 126 pm and of $I^{-}$ ion is 216 pm. The coordination number of $A g^{+}$ ion is :

View Solution

After the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and $∣ ∣ ψ^{2} ∣ ∣$ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.
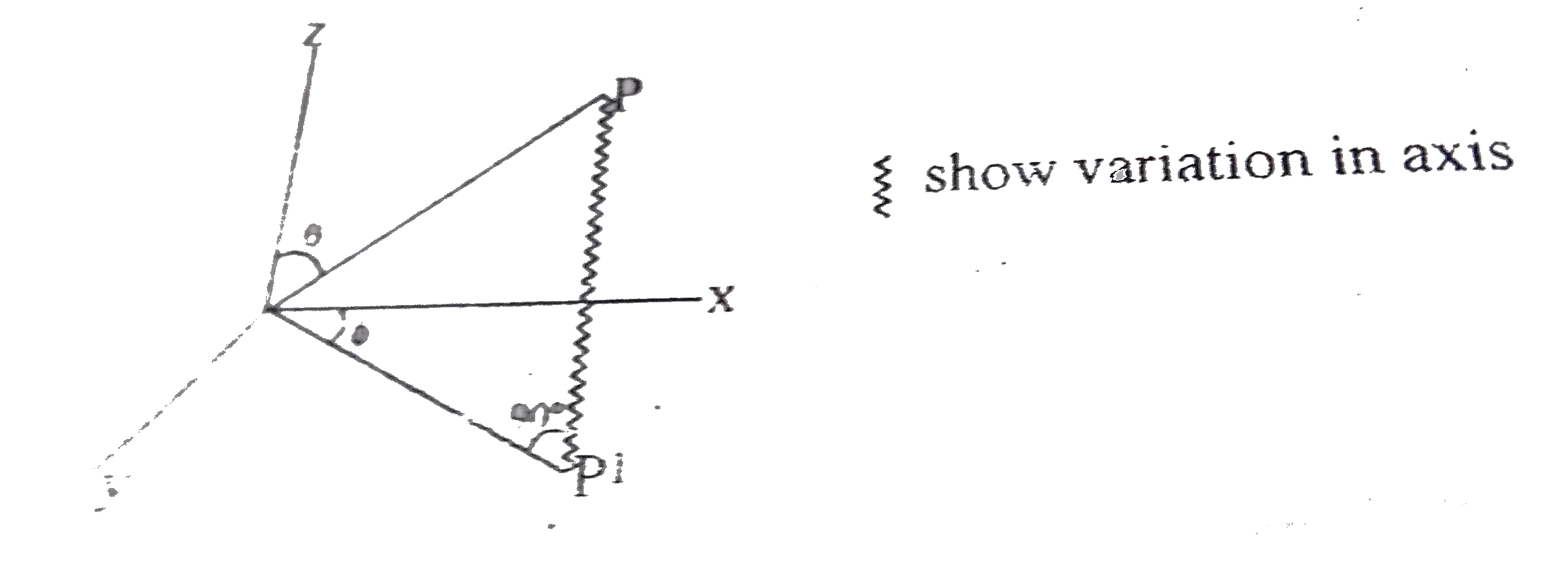
ocr_image
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with $l = 0$ are called s-electrons those occupying orbitals for which $l = 1$ are p-electrons and those for which $l = 2$ are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom $(n = 1, l = 0)$ we have a $1 s$ -electron, or that the electron moves in a $1 s$ -orbital. The relation of the spherical polar co-ordinates $r, θ$ and $ϕ$ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle $θ$ and $ϕ$ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
$ϕ (r, θ, ϕ) = R (r) X (θ, ϕ)$
Angular and radial parts of hydrogen atom wave function
$(Angular part X (θ, ϕ),, Radial part R_{n, l} (r)), (X (s) = {(\frac{1}{4 π})}^{1 / 2},, R (1 s) = 2 {(\frac{z}{a_{0}})}^{3 / 2} e^{- σ / 2}), (X (p_{x}) = {(\frac{3}{4 π})}^{1 / 2} sin θ cos ϕ,, R (2 s) = \frac{1}{2 \sqrt{2}} {(\frac{z}{a_{0}})}^{3 / 2} (2 - σ) e^{- σ / 2}), (X (p_{y}) = {(\frac{3}{4 π})}^{1 / 2} sin θ sin ϕ,, R (2 p) = \frac{1}{2 \sqrt{6}} {(\frac{z}{a_{0}})}^{3 / 2} σ e^{- σ / 2}), (X (p_{z}) = {(\frac{3}{4 π})}^{1 / 2} cos θ,,), (X (d_{2}^{2}) = {(\frac{5}{16 π})}^{1 / 2} (3 {cos}^{2} θ - 1),,), (X (d_{x z}) = {(\frac{15}{4 π})}^{1 / 2} sin θ cos θ cos ϕ,, R (3 s) = \frac{1}{9 \sqrt{3}} {(\frac{z}{a_{0}})}^{3 / 2} (6 - 6 σ + σ^{2}) e^{- σ / 2}), (X (d_{y z}) = {(\frac{15}{4 π})}^{1 / 2} sin θ cos θ sin ϕ,, R (3 p) = \frac{1}{9 \sqrt{6}} {(\frac{z}{a_{0}})}^{3 / 2} (4 - σ) σ e^{- σ / 2}), (X (d_{x^{2} - y^{2}}^{2}) = {(\frac{15}{4 π})}^{1 / 2} {sin}^{2} θ cos 2 ϕ,, R (3 d) = \frac{1}{9 \sqrt{30}} {(\frac{z}{a_{0}})}^{3 / 2} σ^{2} e^{- σ / 2}), (X (d_{x y}) = {(\frac{15}{4 π})}^{1 / 2} {sin}^{2} θ sin 2 ϕ,,), (,, σ = \frac{2 Z r}{n a_{0}}, a_{0} = \frac{h^{2}}{4 π^{2} m e^{2}})$
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, ${(1 / 4 π)}^{1 / 2}$ regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., $ψ^{2}$ at that point. Thus, $ψ^{2}$ is known as probability density and always a positive quantity.
$ψ^{2} d V (or ψ^{2} . 4 π r^{2} d r)$ . represents the probability for finding electron in a small volume dV surrounding the nucleus.
The electron probility density for $1 s$ -orbital best represented by the relation.

View Solution

After the faliure of Bohr atomic theory but its ability to explain to the atomic spectral a need was felt for the new model that could incorporate, the concept of stationary orbit, de Broglie concept, Heisenberg uncertainity principle. The concept that in corporate above facts is called quantum mechanics of the atomic model wave mchanical model. it includes set of quantum number and $∣ ∣ ψ^{2} ∣ ∣$ a mathematical expression of the probability of finding an electron at all points in space. This probability function is the best indication available of how the electon behaves, for as a consequence of the Uncertainity Principle, the amount we can know about the electron is limited. While quantum mechanics can tell us the exact probability of finding an electron at any two particular points, it does not tell us how the electron moves from one of these points to the other. Thus the idea of an electron orbit is lost, it is replaced with a description of where the electron is most likely to be found. This total picture of the probability of finding an electron at various points in space is called an orbital.
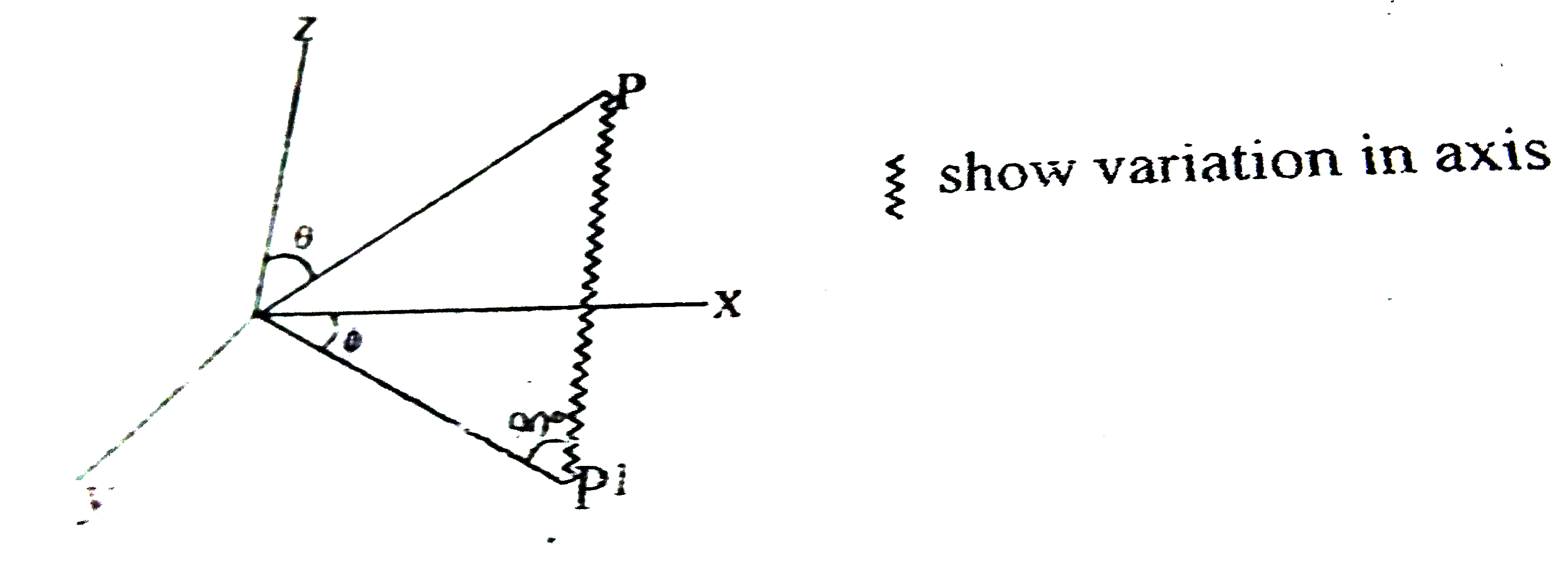
ocr_image
There are various types of orbitals possible, each corresponding to one of the possible combinations of quantum numbers. These orbitals are classified according to the value of n and l associated with them. In order to avoid confusion over the use of two numbers, the numerical velues of l are replaced by letters, electrons in orbitals with $l = 0$ are called s-electrons those occupying orbitals for which $l = 1$ are p-electrons and those for which $l = 2$ are called d-electrons. The numerical and alphabetical correspondences are summarized in table. Using the alphabetical notation for l, we would say that in the ground state of hydrogen atom $(n = 1, l = 0)$ we have a $1 s$ -electron, or that the electron moves in a $1 s$ -orbital. The relation of the spherical polar co-ordinates $r, θ$ and $ϕ$ to Cartesian coordinates x, y and z. To make the concept of an orbital more meaningful, it is helpful to examine the actual solution of the wave function for the one-electron atom. Because of the spherical sysmmetry of the atom, the wave functions are most simply expressed in terms of a spherical polar-coordinate system, shown in fig., which has its orbit at the nucleus. It is found that the wave function can be expressed as the product of two functions, one of which (the ''angular part'' X) depends only the angle $θ$ and $ϕ$ the other of which (the ''radial part'' R) depends only on the distance from the nucleus. Thus we have
$ϕ (r, θ, ϕ) = R (r) X (θ, ϕ)$
Angular and radial parts of hydrogen atom wave function
$(Angular part X (θ, ϕ),, Radial part R_{n, l} (r)), (X (s) = {(\frac{1}{4 π})}^{1 / 2},, R (1 s) = 2 {(\frac{z}{a_{0}})}^{3 / 2} e^{- σ / 2}), (X (p_{x}) = {(\frac{3}{4 π})}^{1 / 2} sin θ cos ϕ,, R (2 s) = \frac{1}{2 \sqrt{2}} {(\frac{z}{a_{0}})}^{3 / 2} (2 - σ) e^{- σ / 2}), (X (p_{y}) = {(\frac{3}{4 π})}^{1 / 2} sin θ sin ϕ,, R (2 p) = \frac{1}{2 \sqrt{6}} {(\frac{z}{a_{0}})}^{3 / 2} σ e^{- σ / 2}), (X (p_{z}) = {(\frac{3}{4 π})}^{1 / 2} cos θ,,), (X (d_{2}^{2}) = {(\frac{5}{16 π})}^{1 / 2} (3 {cos}^{2} θ - 1),,), (X (d_{x z}) = {(\frac{15}{4 π})}^{1 / 2} sin θ cos θ cos ϕ,, R (3 s) = \frac{1}{9 \sqrt{3}} {(\frac{z}{a_{0}})}^{3 / 2} (6 - 6 σ + σ^{2}) e^{- σ / 2}), (X (d_{y z}) = {(\frac{15}{4 π})}^{1 / 2} sin θ cos θ sin ϕ,, R (3 p) = \frac{1}{9 \sqrt{6}} {(\frac{z}{a_{0}})}^{3 / 2} (4 - σ) σ e^{- σ / 2}), (X (d_{x^{2} - y^{2}}^{2}) = {(\frac{15}{4 π})}^{1 / 2} {sin}^{2} θ cos 2 ϕ,, R (3 d) = \frac{1}{9 \sqrt{30}} {(\frac{z}{a_{0}})}^{3 / 2} σ^{2} e^{- σ / 2}), (X (d_{x y}) = {(\frac{15}{4 π})}^{1 / 2} {sin}^{2} θ sin 2 ϕ,,), (,, σ = \frac{2 Z r}{n a_{0}}, a_{0} = \frac{h^{2}}{4 π^{2} m e^{2}})$
This factrorization helps us to visualize the wave function, since it allows us to consider the angular and radial dependences separately. It contains the expression for the angular and radial parts of the one electron atom wave function. Note that the angular part of the wave function for an s-orbital it alwats the same, ${(1 / 4 π)}^{1 / 2}$ regardless of principal quantum number. It is also true that the angular dependence of the p-orbitals and of the d-orbitals is independent of principle quantum number. Thus all orbitals of given types (s, p, or d) have the same angular behavour The table shows, however, that the radial part of the wave function depends both on the principal quantum n and on the angular momentum quantum number l.
To find the wave function for a particular state, we simply multiply the appropriate angular and radial parts togather called normalized wave function.
The probability of finding an electron at a point within an atom is proportional to the square of orbital wave function, i.e., $ψ^{2}$ at that point. Thus, $ψ^{2}$ is known as probability density and always a positive quantity.
$ψ^{2} d V (or ψ^{2} . 4 π r^{2} d r)$ . represents the probability for finding electron in a small volume dV surrounding the nucleus.
The angular wave function of which orbital with not disturb by the variation with azimuthal angle only

View Solution

Early crystallographers had trouble solving the structures of inorganic solids using X-ray diffraction because some of the mathematical tools for analyzing the data had not yet been developed. Once a trial structure was proposed, it was relatively easy to calculate the diffraction pattern, but it was difficult to go the other way (from the diffraction pattern to the structure) if nothing was known a priori about the arrangement of atoms in the unit cell. It was important to develop some guidelines for guessing the coordination numbers and bonding geometries of atoms in crystals. The first such rules were proposed by Linus Pauling, who considered how one might pack together oppositely charged spheres of different radii.
Pauling proposed from geometric considerations that the quality of the "fit" depended on the radius ratio of the anion and the cation.
If the anion is considered as the packing atom in the crystal, then the smaller catin fills interstitial sites ("holes"). Cations will find arrangements in which they can contact the largest number of anions. If the cation can touch all of its nearest neighbour anions then the fit is good. If the cation is too small for a given site, that coordination number will be unstable and it will prefer a lower coordination structure. The table below gives the ranges of cation/anion radius ratios that give the best fit for a given coordination geometry.
$\begin{matrix} Coordiantion number & Geometry & ρ = \frac{r_{cation}}{r_{amion}} 2 & linear & 0 - 0.155 3 & triangular & 0.155 - 0.225 4 & tetrahedral & 0.225 - 0.414 4 & square planar & 0.414 - 0.732 6 & octahedral & 0.414 - 0.732 8 & cubic & 0.732 - 1.0 12 & cuboctahedral & 1.0 \end{matrix}$
(Source : Ionic Radii and Radius Ratios. (2021, June 8). Retrieved June 29, 2021, from https://chem.ibretexts.org/@go/page/183346)
A solid AB has square planar structure. If the radius of cation $A^{+}$ is 120 pm, calculate the maximum possible value of anion $B^{-}$ .

View Solution

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

Consider a plane $x + y - z = 1$ and point $A (1, 2, - 3)$ . A line L has the equation $x = 1 + 3 r, y = 2 - r and z = 3 + 4 r$ .
The coordinate of a point B of line L such that AB is parallel to the plane is

A2Z-CHEMICAL COORDINATION AND INTEGRATION-Section D : Chapter-end Test

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

Consider a plane x+y−z=1 and point A(1,2,−3). A line L has the equation x=1+3r,y=2−randz=3+4r. The coordinate of a point B of line L such that AB is parallel to the plane is

A2Z-CHEMICAL COORDINATION AND INTEGRATION-Section D : Chapter-end Test

Consider a plane $x + y - z = 1$ and point $A (1, 2, - 3)$ . A line L has the equation $x = 1 + 3 r, y = 2 - r and z = 3 + 4 r$ .
The coordinate of a point B of line L such that AB is parallel to the plane is