Two audio speakers are kept some distance apart and are driven by the same amplifier system. A person is sitting at a place 6.0 m from one of the speakers and 6.4 m from the other. If the sound signal is continuously varied from 500 Hz to 5000 Hz, what are the frequencies for which there is a destructive interference at the place of the listener? Speed of sound in air=320ms−1
The correct Answer is:1200 Hz, 2000 Hz, 2800 Hz, 3600 Hz and 4400 Hz
Path difference = 6.4 - 6 = 0.4 m
high wavelength = vnL=320500=0.64)
low wavelength = vnH=3205000=0.064m
Destructive interference occures when
Δ=(2n+1)λ2
0.4=(2n+1)λ2
λ=0.82n+1
Thus coresponding frequencies are
n=320λ=3200.8×(2n+1)
= 400(2n + 1)
= 400 Hz, 1200 Hz, 2000 Hz, 2800 Hz, 4400 Hz, 5200 Hz,....
Topper's Solved these Questions
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Practice Exercise 6.4
10 Videos
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Practice Exercise 6.5
16 Videos
- WAVES BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVES EXERCISE - Practice Exercise 6.2
11 Videos
- WAVE OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WAVE OPTICSEXERCISE - Unsolved Numerical Problems
28 Videos
- X-RAYSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - X-RAYSEXERCISE - Unsolved Numerica Problem for Preparation
23 Videos
Similar Questions
A person has a hearing range from 20Hz to 20kHz. What are the typical wavelength of sound waves in sir corresponding to these two frequencies ? Take the speed of sound in air as 344m/s.
View SolutionTwo sources are placed from a person P as shown in figure. The speed of sound in air is 320m/s.
(a)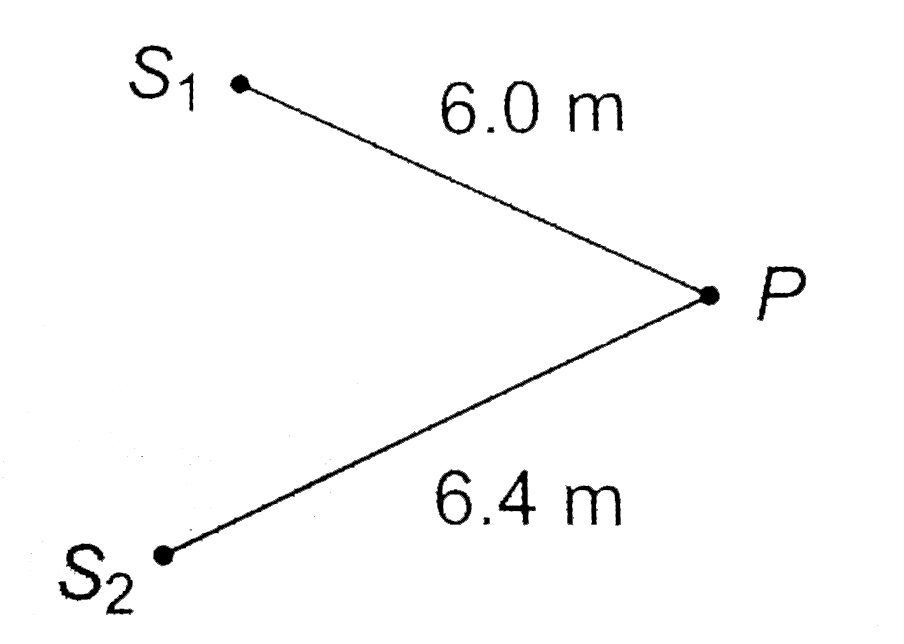
If sound signal is continuously varied from 500Hz to 2500Hz, for which frequency listener will hear minimum sound intensity.
(b)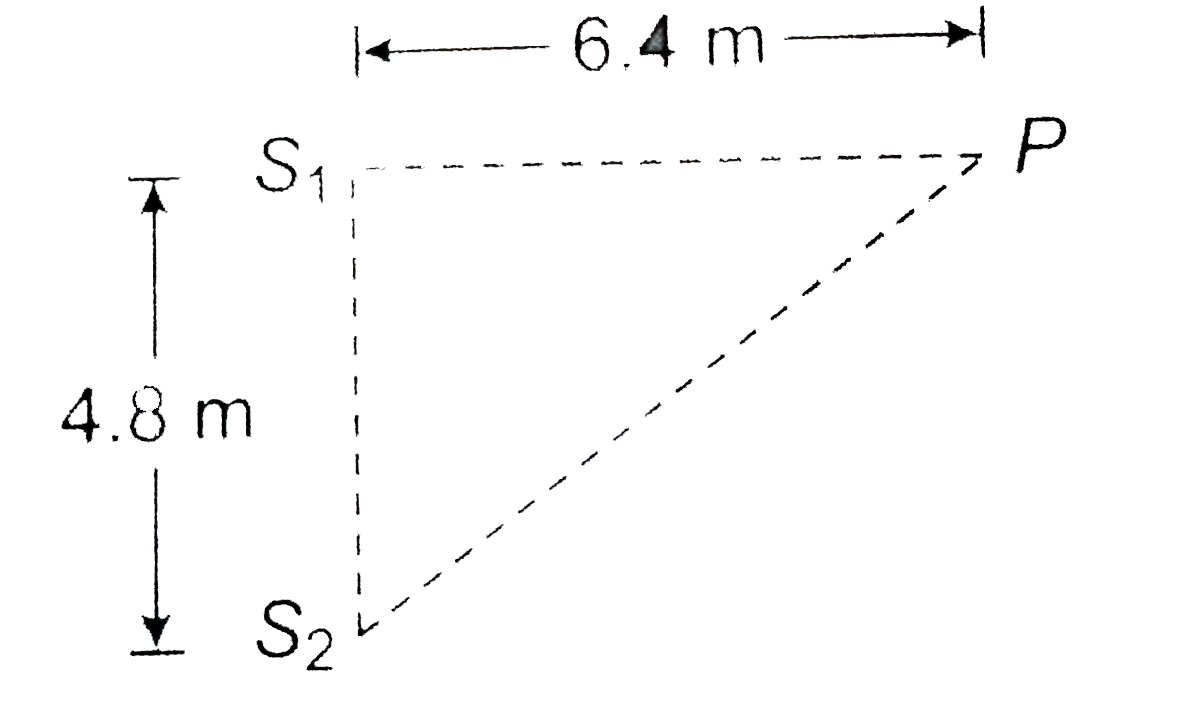
Find the frequencies in audible range (20−20000Hz) for which listener will hear maximum sound intensity.
View Solution
Knowledge Check
Two bodies of masses m and 2m are kept at distance r apart from each other. Then the value of G varies as
Ar2Br4Cr−2DrthTwo loudspeakers are located 3 m apart on the stage of an auditorium. A listener at point P is seated 29.0 m from one speaker and 25.0 m from the other. A signal generator drives the speakers in phase with the same amplitude and frequency. The wave amplitude at P due to each speaker alone is A. The frequency is then varied between 20 Hz and 300 Hz. The speed of sound is 343 m/s.
At what frequency or frequencies will the listener at P hear a maximum intensity?A170 Hz onlyB57 Hz, 113 Hz, 170 Hz, 227 Hz, and 284 HzC113 Hz and 226 HzD86 Hz, 170 Hz, 257 HzTwo loudspeakers are located 3 m apart on the stage of an auditorium. A listener at point P is seated 29.0 m from one speaker and 25.0 m from the other. A signal generator drives the speakers in phase with the same amplitude and frequency. The wave amplitude at P due to each speaker alone is A. The frequency is then varied between 20 Hz and 300 Hz. The speed of sound is 343 m/s.
Determine the value of the maximum amplitude in terms of A.A2.0AB3.0 AC2.5 AD4.0A
Figure 7.20 shows a tube structure in which signal is sent from one end and is received at the other end . The frequency of the sound source can be varied electronically between 2000→5000Hz. Find the frequencies at which maxima of intensity are detected . The speed of sound in air 340m/s.
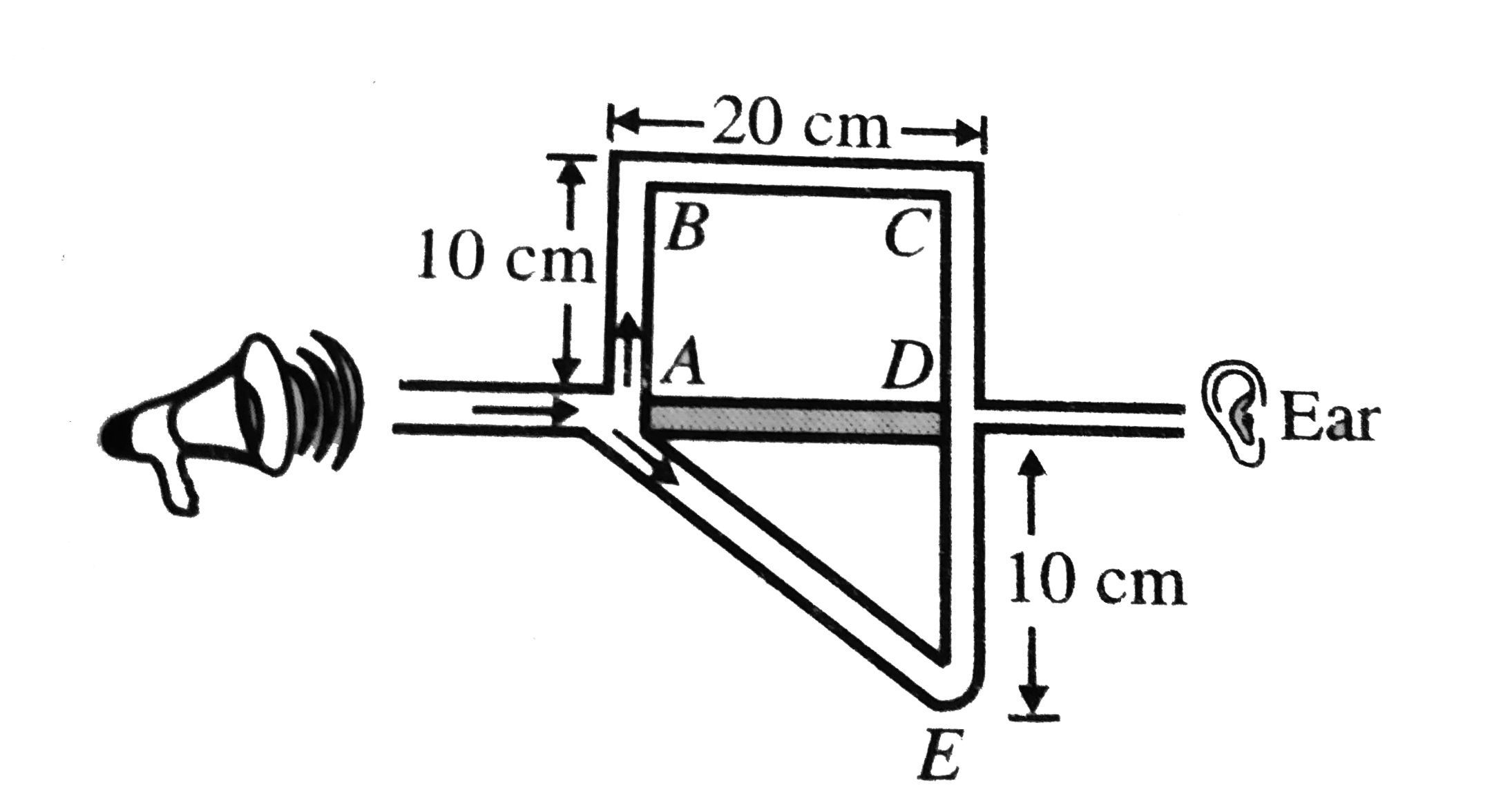
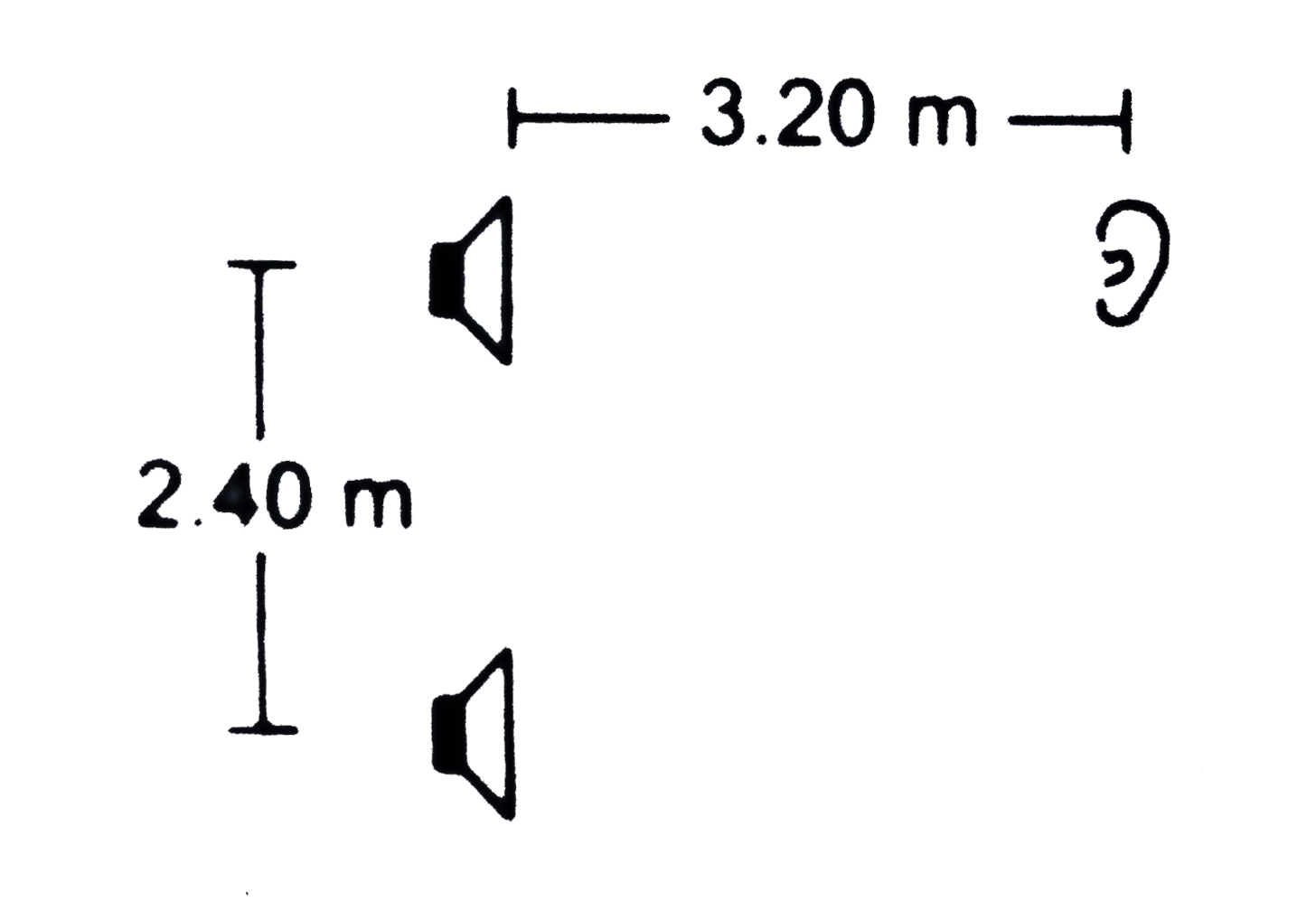
View SolutionTwo stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air =320ms−1
View SolutionA person has a hearing range from 20Hz to 20kHz. What are the typical wavelength of sound waves in sir corresponding to these two frequencies ? Take the speed of sound in air as 344m/s.
View SolutionAn operator sitting in his base camp sends a sound signal of frequency 400 Hz. The signal is reflected back from a car moving towards him The frequency of the reflected sound is found to be 410 Hz. Find the speed of the car. Speed of sound in air=324ms−1.
View SolutionTwo stereo speaks S1andS2 are separated by a distance of 2.40m. A person (P) is at a distance of 2.40m. A person (P) is at a distance of 3.20m directly in front of one of the speakers as shown in Fig. 7.8. Find the frequencies in the audible range (20−20,000Hz) for which the listener will hear a minimum sound intensity . Speed of sound in air = 320 m//s.
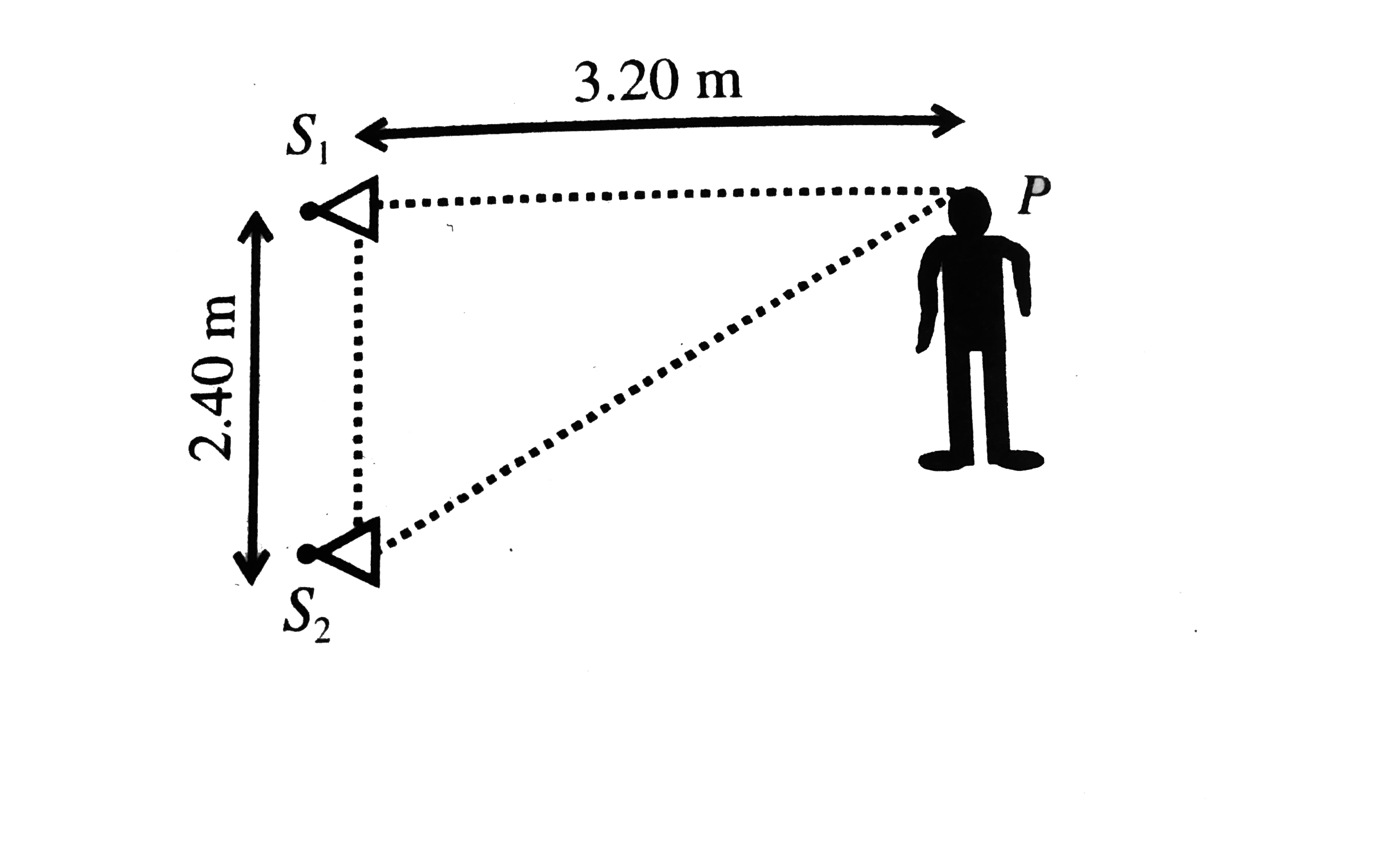
View Solution
