A block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength $λ_{0}$ is produced at the lower of the rope.

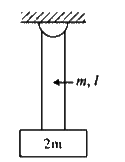
The time taken by the pulse to reach the other end of the rope is:

A

$2 \sqrt{\frac{l}{g}} (\sqrt{3} - 1)$

B

$2 \sqrt{\frac{l}{g}} (\sqrt{3} - 2)$

C

$2 \sqrt{\frac{l}{g}}$

D

$2 \sqrt{\frac{l}{g}} (\sqrt{3} - \sqrt{2})$

Text Solution

Verified by Experts

The correct Answer is:D

Let $v_{x}$ be speed of pulses x distance from bottom of rope
Then $v_{x} = \sqrt{(2 m + \frac{max}{l}) \frac{g}{m / l}} = \sqrt{(2 l + x)} g$
Then time taken to go from bottom to top will be
T = $L \int 0 \frac{d x}{\sqrt{(2 l + x)} g} = 2 \sqrt{\frac{l}{g}} (\sqrt{3} - \sqrt{2})$ .

|

Updated on:21/07/2023

Class 12 PHYSICS WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength $λ_{0}$ is produced at the lower of the rope.

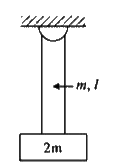
The wavelength of the pulse when it reaches the other end of the rope is :
A $\sqrt{3} λ_{0}$
B $\sqrt{\frac{3}{2}} λ_{0}$
C $λ_{0}$
D $\frac{λ_{0}}{2}$
Question 2 - Select One
A block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength $λ_{0}$ is produced at the lower of the rope.

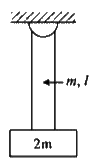
The speed of the pulseat the mid point of rope is:
A $\sqrt{\frac{5}{2}} g l$
B $\sqrt{\frac{3}{3}} g l$
C $\sqrt{\frac{2}{5}} g l$
D $\sqrt{\frac{g l}{2}}$
Question 3 - Select One
A uniform rope of length $L$ and mass $m_{1}$ hangs vertically from a rigid support. A block of mass $m_{2}$ is attached to the free end of the rope. A transverse pulse of wavelength $λ_{1}$ is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is $λ_{2}$ . The ratio $\frac{λ_{2}}{λ_{1}}$ is
A $\sqrt{\frac{m_{1}}{m_{2}}}$
B $\sqrt{\frac{m_{1} + m_{2}}{m_{2}}}$
C $\sqrt{\frac{m_{2}}{m_{1}}}$
D $\sqrt{\frac{m_{1} + m_{2}}{m_{1}}}$

PHYSICS GALAXY - ASHISH ARORA-WAVES -Numerical MCQs Single Options Correct

Home
Ask Doubt
Profile