A standing wave exists in string of length 150 cm fixed at both ends. The displacement amplitude of a point at a distance of 10 cm from one of ends if $5 \sqrt{3} m m$ . The distance between two nearest points, within the same loop having the same displacement amplitude of $5 \sqrt{3}$ is 10 nm.
The maximum displacement amplitude of the particle in the string is,:

A

2

B

3

C

4

D

6

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Given displacement amplitude of a point 10 cm from end is $5 \sqrt{3} m$ m.
Also distance with same loop between two point with
displacement amplitude $5 \sqrt{3}$ is also 10 cm. Then
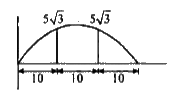By symmetry, $\frac{λ}{2} = 30 c m$
$λ = 60 c m$
Now $λ \to 2 p \to 60 c m$
$10 c m \to \frac{λ}{6} = \frac{2 π}{6} = \frac{π}{3}$
$A sin \frac{π}{3} = 5 \sqrt{3}$
$A = \frac{5 \sqrt{3}}{\sqrt{3} / 2} = 10 m m$
Since there will be 5 loops in string, string is in $4^{t h}$ overtone. Potential energy of string will be zero at antinodes, which will be 15 cm from one end.

|

Updated on:21/07/2023

Class 12 PHYSICS WAVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A string of length $' l'$ is fixed at both ends. It is vibrating in its $3^{r d}$ overtone with maximum ampltiude $' a'$ . The amplitude at a distance $\frac{l}{3}$ from one end is $= \sqrt{p} \frac{a}{2}$ . Find $p$ .
A $a$
B $0$
C $\frac{(\sqrt{3} a)}{2}$
D $\frac{a}{2}$
Question 2 - Select One
A string of length l is fixed at both ends. It is vibrating in its $3^{r d}$ overtone with maximum amplitude 'a'. The amplitude at a distance l/3 from one end is
Aa
B0
C $\frac{\sqrt{3 a}}{2}$
D $\frac{a}{2}$
Question 3 - Select One
A string of length 1.5 m with its two ends clamped is vibrating in fundamental mode. Amplitude at the centre of the string is 4 mm. Minimum distance between the two points having amplitude 2 mm is:
A $1 m$
B $75 c m$
C $60 c m$
D $50 c m$

PHYSICS GALAXY - ASHISH ARORA-WAVES -Numerical MCQs Single Options Correct

Home
Ask Doubt
Profile