The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs(i) none(ii) not more than one(iii) more than one(iv) at least onewill fuse after 150 days of use.
Let X = number of fuse bulbs. p = probability of a bulb produced by a factory will fuse after 150 days of use.
∴p=0.05andq=1–p=1–0.05=0.95
Given: n=5<br>∴X~B(5,0.05)
(i) P(none of a bulb produced by a factory will fuse after 150 days of use) = P[X = 0]
P(no≠)=P(X=0)=5C^0(0.95)5⋅(0.05)0
=1×(0.95)5=(0.95)5
P(not more than one bulb will fuse after 150 days of j use) = P[X ≤ 1]
=P(X=0)+P(X=1)
=^5C0(0.95)5×(0.05)0+5C10.95^4×(0.05)1
=1×(0.95)5+5×(0.95)4×(0.05)
=(0.95)5+(0.25)(0.95)4
=(0.95)4[0.95+0.25]
=(0.95)4×1.2
(iii) P(more than one bulb fuse after 150 days) = P[X > 1]
=1−P(X≤1)
=1−P(notmorethan1)
=1−(0.95)4×1.2
(iv) P(atleastone)=P(X≥1)
=1−P(X<1)
=1−P(X=0)
=1−5C0(0.95)5×(0.05)0
=1−1×(0.95)5
=1−(0.95)5
Topper's Solved these Questions
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - EXERCISE 13.218videos
PROBABILITY
- BOOK - NCERTCHAPTER - PROBABILITYEXERCISE - MISCELLANEOUS EXERCISE19videos
PROBABILITY
- BOOK - NCERTCHAPTER - MATRICESEXERCISE - EXERCISE 3.312videos
MATRICES
- BOOK - NCERTCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 1.314videos
RELATIONS AND FUNCTIONS
Similar Questions
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs :
(i) none
(ii) none more than one
(iii) more than one
(iv) at least one
will fuse after 150 days of use.View SolutionThe probability that a bulb produced by a factory will fuse after an year of use is 0.1. Then the probability that out of 4 such bulbs, only one is working after an year
View Solution
Knowledge Check
- Question 1 - Select One
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. What is the probability that out of 5 such bulbs none will fuse after 150 days of use?
A1−(1920)5B(1920)5C(34)5D90(14)5 - Question 2 - Select One
The probability that tulb produced by a factor will fuse after 150 days if used is 0.50. What is the probability that out of 5 such balbs none will fuse after 150 days of use ?
A1−(19/20)5B(19/20)5C(3/4)5D90(1/4)5
The probability that a bulb produced by a factory will fuse after 160 days of use is 0.06. Find the probability that out of 5 such bulbs at the most one bulb will fuse after 160 days of use.
View SolutionThe probability that a bulb produced by a factory will fuse after 6 months of use is 0.05 . Find the probability that out of 5 such bulbs
(i) none will fuse after 6 months of use
(ii) at least one will fuse after 6 months of use
(iii) not more than one will fuse after 6 months of use.View SolutionThe probability that a bulb produced by a factory will fuse after 150 days if used is 0.05. what is the probability that out of 5 such bulbs none will fuse after 150 days of use? 1−(1920)5 b. (1920)5 c. (34)5 d. 90(14)5
View SolutionThe probability that a bulb produced by a factory will fuse after 200 days of use is 0.2. Let X denote the number of bulbs (out of 5 ) that fuse after 200 days of use . Find the probability of
(i)X=0,(ii)X≤1,(iii)X>1,(iv)X≥1.View SolutionThe probability that the life of a bulb is 100 days is 0.05. Find the probability that out of 6 bulbs (i) atleast 1 (ii) greater than 4 (iii) none will be having a life of 100 days
View SolutionThe probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. If a sample of such 5 bulbs are taken out, then match the probabilities in column I with their respective values in column II and choose the correct option from the codes given below.
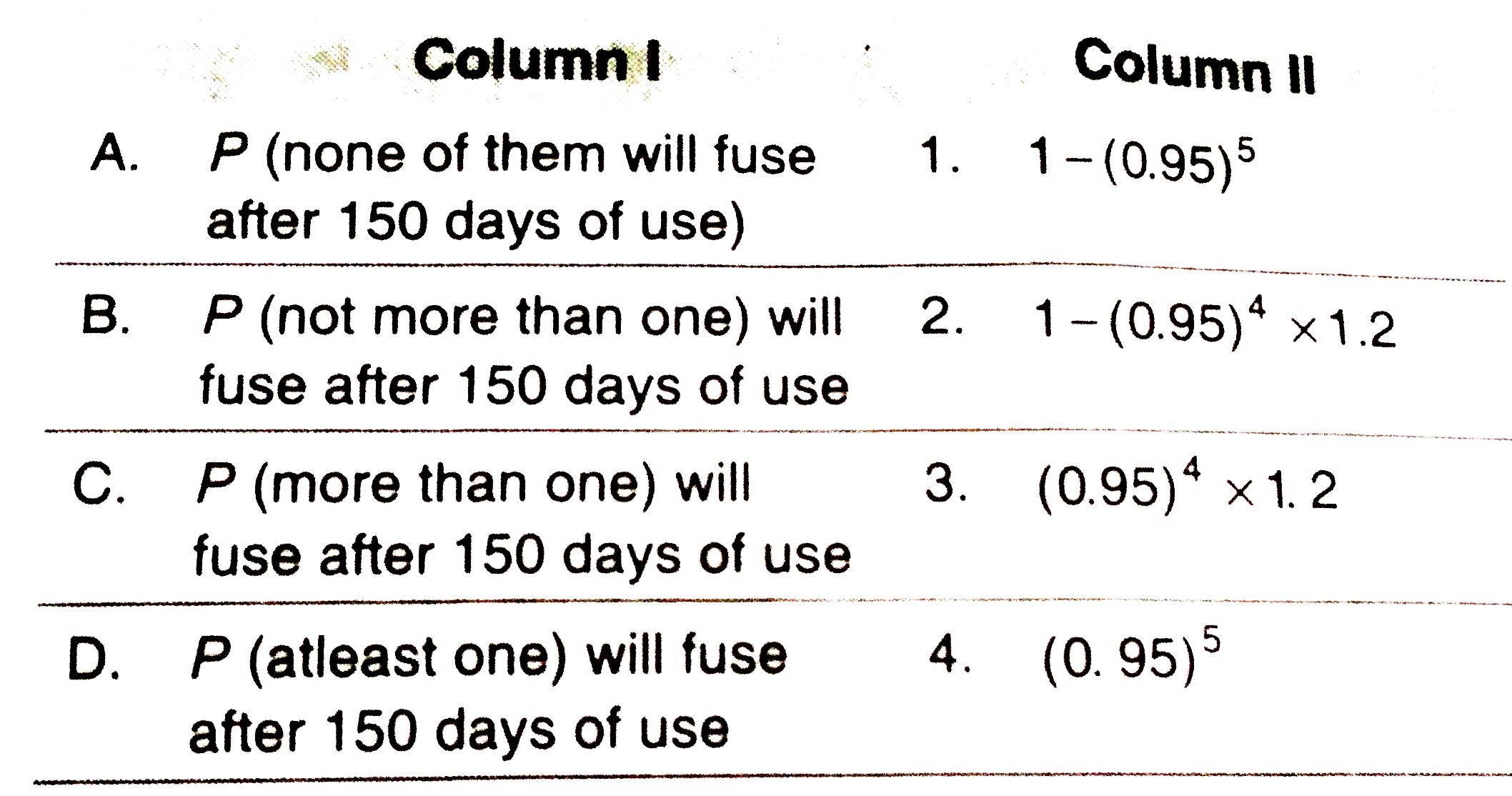 View Solution
View Solution

