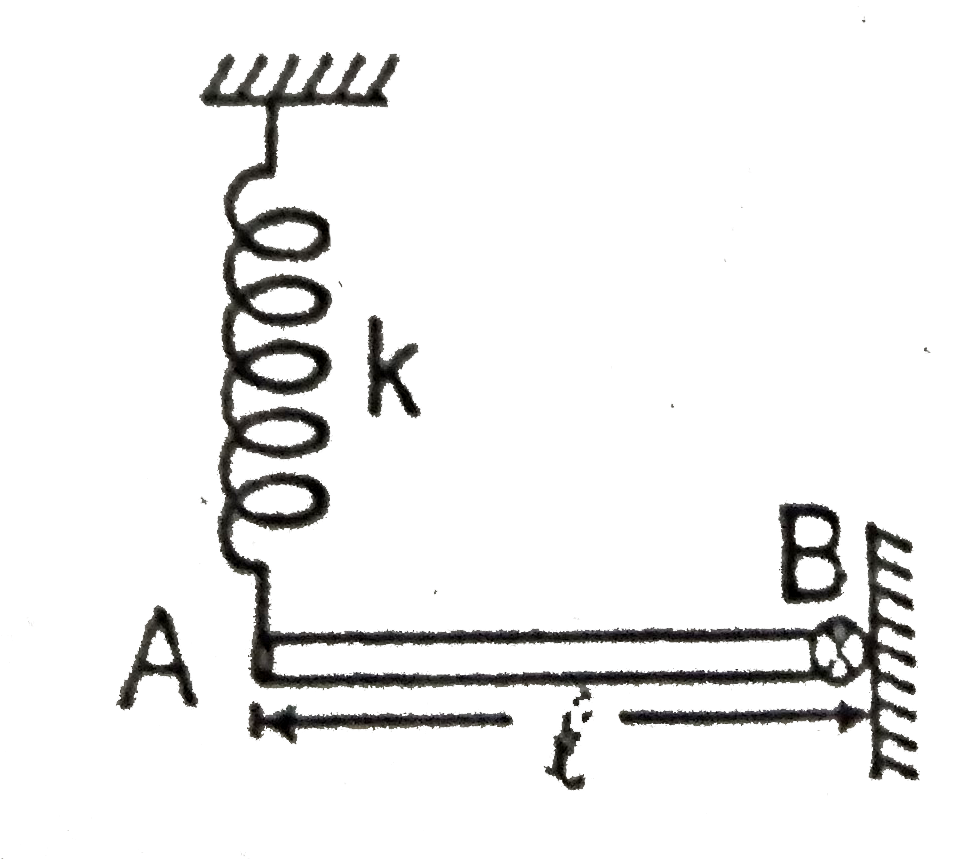
AB is a massless frictionless glass rod which can slide on the U-frame XX', with the help of two frictionless rings. A water film is formed between the rod and the U-shaped frame. The rod is held in equilibrium by a hair- spring of stiffness k. Surface tension of water is T and length of rod AB is L. Find the extension in the spring.
Step by step video & image solution for AB is a massless frictionless glass rod which can slide on the U-frame XX', with the help of two frictionless rings. A water film is formed between the rod and the U-shaped frame. The rod is held in equilibrium by a hair- spring of stiffness k. Surface tension of water is T and length of rod AB is L. Find the extension in the spring. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Similar Questions
A rigid bent light rod of total length 2l can slide on fixed wire frame with the help of frictionless sliders. There is thin liquid film (surface tension T) between bent rod and wire frame. In equilibrium the elongation in spring is given by (4Tlα5K). then find the value of α.
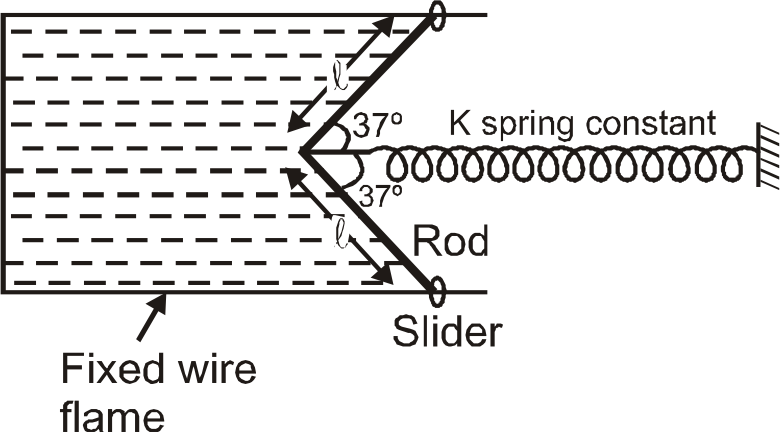 View Solution
View SolutionA wheel is mounted on frictionless central pivot and it can rotate freely in the vertical plane. There is a horizontal light rod fixed to the wheel below the pivot. There is a small sleeve of mass m which can slide along the rod without friction. The sleeve is connected to a light spring. The other end of the spring is fixed to the rim as shown. The sleeve is at the centre of the rod and the spring is relaxed. Now the wheel is held at rest and the sleeve is moved towards left so as to compress the sprig by some distance. The sleeve and the wheel are released simultaneously from this position.
(a) Is it possible that the wheel does not rotate as the sleeve perform SHM on the rod ?
(b) Find the value of spring constant k for situation described in (a) to be possible. The distance of rod from centre of the wheel is d.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
An L shaped uniform rod of mass 2M and length 2L(AB=BC=L) is held as shown in Fig. with a string fixed between C and wall so that AB is vertical and BC is horizontal. There is no friction between the hinge and the rod at A.
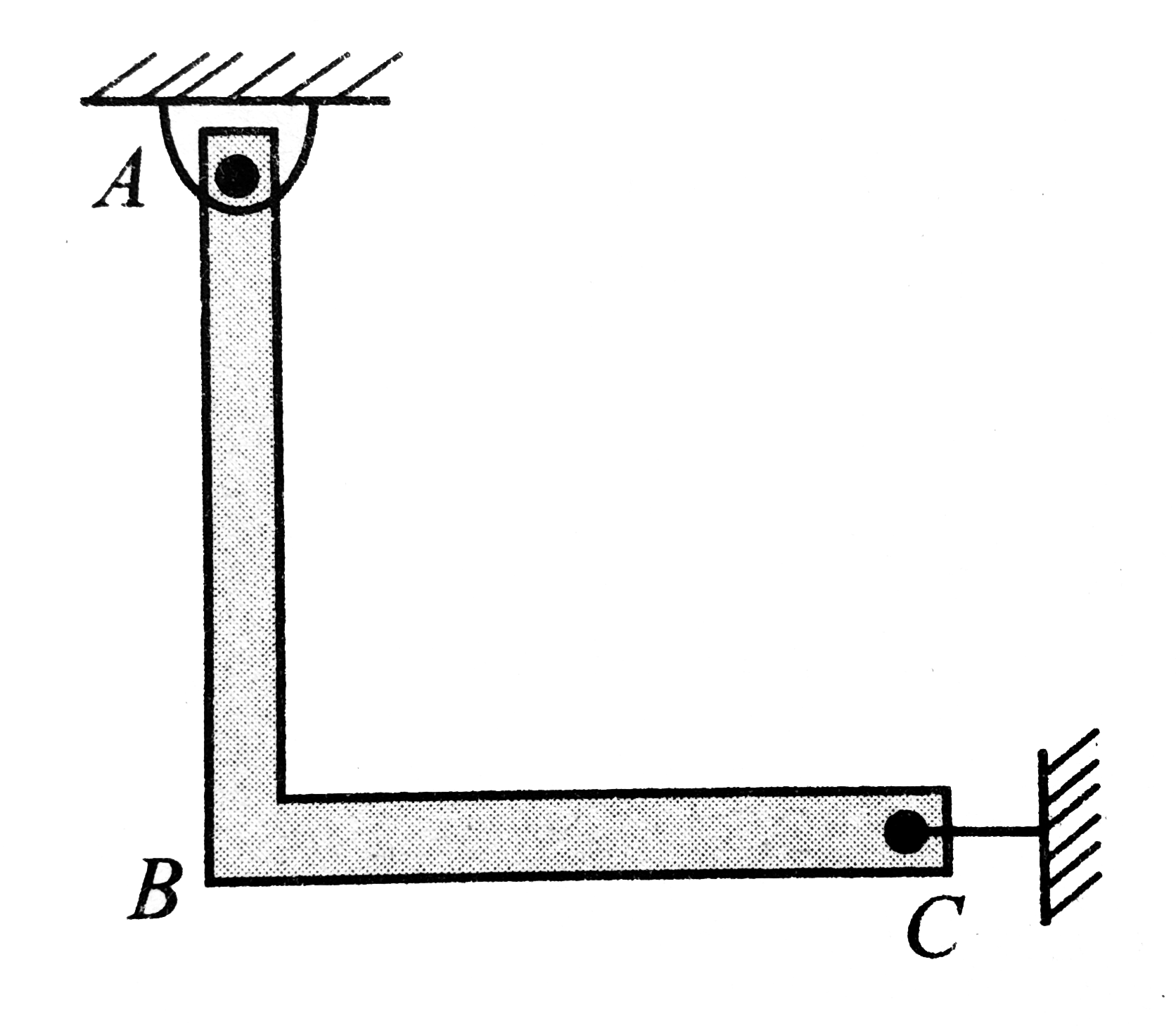
Find the tension in the stringAMg3BMg4CMgDMg2 - Question 2 - Select One
A rod of mass 'M' and length'
L' is hinged about one end and a
particle of mass 'M' is
attached to its other end If it is
kept horizontal with the help of
a spring of spring constant 'K'
as shown in fig. find the
extension in spring :-
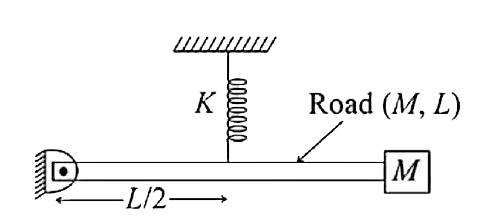 A3MgKBMgKC2MgKD4MgK
A3MgKBMgKC2MgKD4MgK - Question 3 - Select One
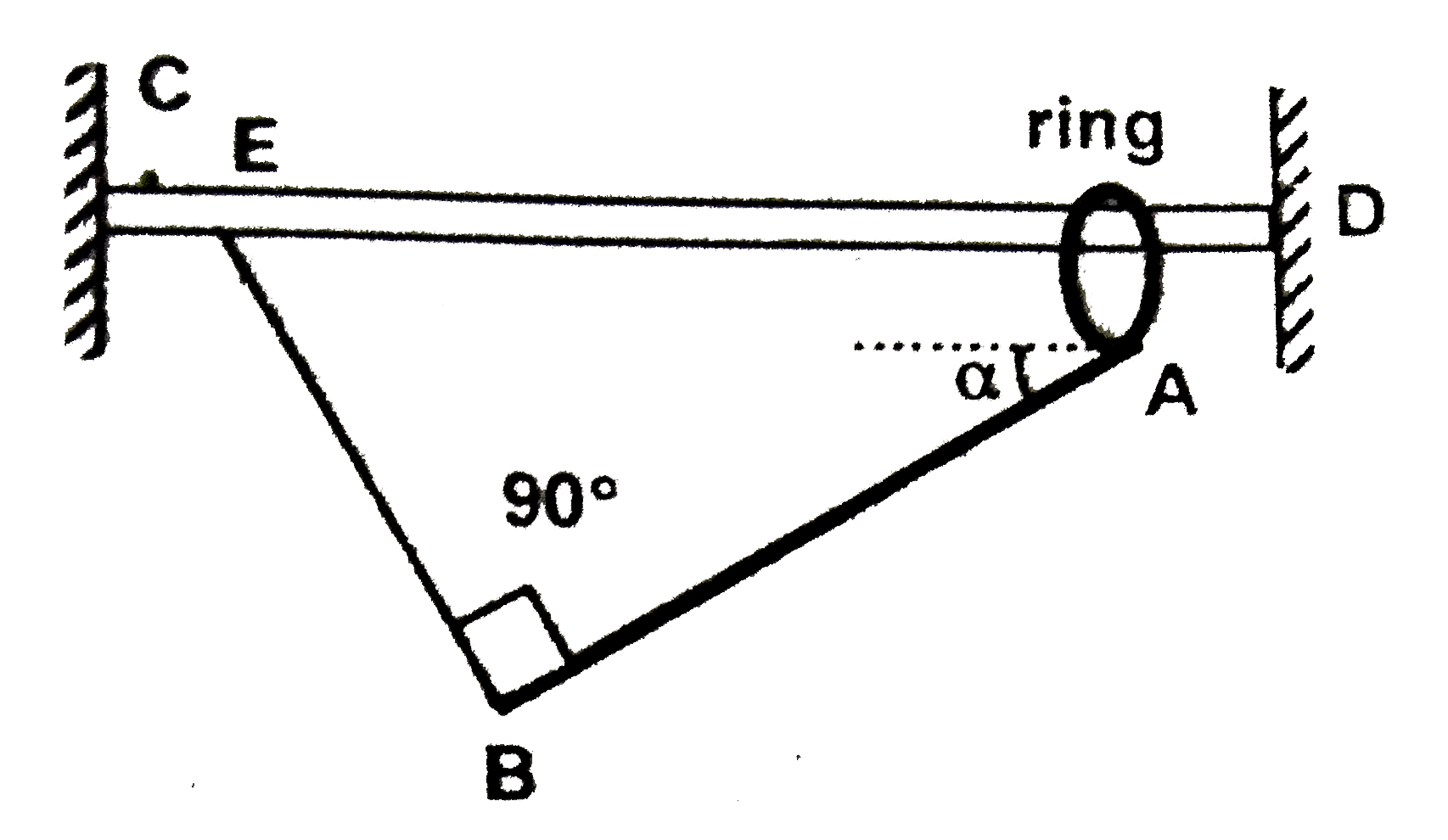
One end of a heavy uniform rod AB can slide along rough horizontal guiding surface CD with the help of massless ring as shown in the figure. The dimension of ring is negligible. BE is the ideal string if ∠EBA is right angle and α is the angle between rod AB and horizontal when the rod is on the verge of sliding. Find the coefficient of friction between ring and horizontal guiding surface CD.Atanα2+tan2αBtanα1+2tan2αCtanα2−tanαDtanα1−tan2α
A square hinged -structure (ABCD) is formed with four massless rods which lie on the smooth horizontal table. The hinge−D of structure is fixed with table and hinge A, hinge −B and hinge-C are free to move on the table. A point mass m is attached at hinge −B, and an ideal spring of stiffness k is connected between hinge −A and hinge-C as shown in the figure. System is in equilibrium. The mass m is slightly along line BD and released to perform SHM. The time period of SHM is π√nmk. Find
 View Solution
View SolutionA light rod AB is fitted with a small sleeve of mass m which can slide smoothly over it. The sleeve is connected to the two ends of the rod using two springs of force constant 2k and k (see fig). The ends of the springs at A and B are fixed and the other ends (connected to sleeve) can move along with the sleeve. The natural length of spring connected to A is l0. Now the rod is rotated with angular velocity w about an axis passing through end A that is perpendicular to the rod. Take kmω2=η and express the change in length of each spring (in equilibrium position of the sleeve relative to the rod) in terms of l0 and η.
 View Solution
View SolutionIn the figure a uniform rod of mass 'm' and length 'l' is hinged at one end and the other end is connected to a light vertical of spring constant 'k' as shown in figure. The spring has extension such that rod is equilibrium when it is horizontal . The rod rotate about horizontal axis passing through end 'B'. Neglecting friction at the hinge find (a) extension in the spring (b) the force on the rod due to hinge.
 View Solution
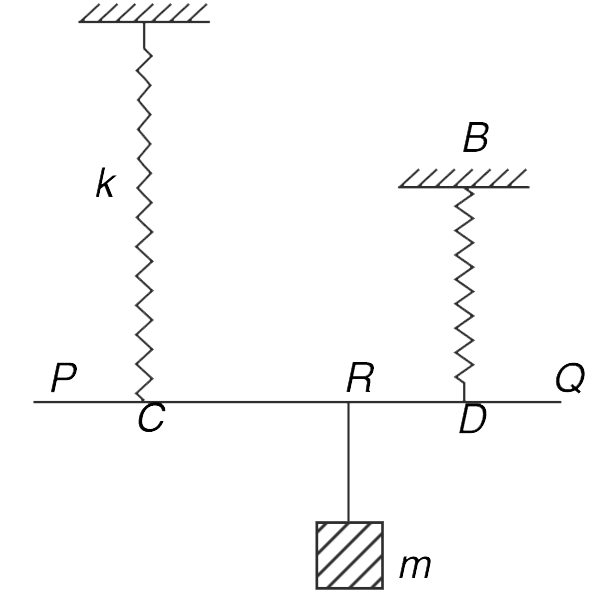
View SolutionTwo ideal springs of same make (the springs differ in their lengths only) have been suspended from points A and B such that their free ends C and D are at same horizontal level. A massless rod PQ is attached to the ends of the springs. A block of mass m is attached to the rod at point R. The rod remains horizontal in equilibrium. Now the block is pulled down and released. It performs vertical oscillations with time period T=2π√m3k where k is the force constant of the longer spring.
(a) Find the ratio of length RC and RD.
(b) Find the difference in heights of point A and B if it is given that natural length of spring BD is L.
 View Solution
View SolutionA glass prism has its principal section in form of an equilateral triangle of side length l. The length of the prism is L (see fig.). The prism, with its base horizontal, is supported by a vertical spring of force constant k. Half the slant surface of the prism is submerged in water. Surface tension of water is T and contact angle between water and glass is 0∘. Density of glass is d and that of water is ρ(<d). Calculate the extension in the spring in this position of equilibrium.
 View Solution
View Solution
