A rod flies with constant velocity past a mark which is stationary in the reference frame K. In the frame K it takes Δt=20ns for the rod to fly past the mark. In the reference frame fixed to the rod the mark moves past the rod of Δt′=25ns. Find the proper length of rod.
In the frame K the length l of the rod is related to the time of flight Δt by
l=vΔt′
But l0=l√1−β2=vΔt√1−β2, β=vc
Thus, vΔt′=vΔt√1−β2
So 1−β2=(ΔtΔt′)2 or v=c√1−(ΔtΔt′)2
and l0=c√(Δt′)2−(Δt)2=cΔt′√1−(ΔtΔt′)2
Topper's Solved these Questions
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Hydrodynamics
25 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Transport Phenomena
38 Videos
Similar Questions
A rod moves along a ruler with a constant velocity. When the positions of both ends of the rod are marked simultaneously in the reference frame fixed to the rule, the difference of readings on the rule is equal to Δx1=4.0m. But when the positions of the rod's ends are marked simultaneously in the reference frame fixed to the rod, the difference of readings on the same ruler is equal to Δx2=9.0m. Find the proper length of the rod and its velocity relative to the ruler.
View SolutionA rod moves lengthwise with a constant velocity v relative to the inertial reference frame K. At what value of v will the length of the rod in this frame be η=0.5% less than its proper length?
View Solution
Knowledge Check
A frame of reference which moves with constant velocity with reference to a stationary frame of reference is called______________.
Ainertial frame of referenceBnon-inertial frame of referenceCrotating frame of referenceDabsolute frame of reference
Two unstable particles move in the reference frame K along a straight line in the same direction with a velocity v=0.990c. The distance between them in this reference frame is equal to l=120m. At a certain moment both particles decay simultaneously in the reference frame fixed to them. What time interval between the moments of decay of the two particles will be observed in the frame K? Which particle decays later in the frame K?
View SolutionWith what velocity (relative to the reference frame K) did the clock move, if during the time interval t=5.0s, measured by the clock of the frame K, it becomes slow by Δt=0.10s?
View SolutionThe reference frame, in which the centre of inertia of a given system of particles is at rest, translates with a velocity V relative to an inertial reference frame K. The mass of the system of particles equals m, and the total energy of the system in the frame of the centre of inertia is equal to ˜E. Find the total energy E of this system of particles in the reference frame K.
View SolutionA rod AB oriented along the x axis of the reference frame K moves in the positive direction of the x axis with a constant velocity v. The point A is the forward end of the rod, and the point B its near end. Find:
(a) the proper length of the rod, if at the moment tA the coorniate of the point A is equal to xA, and at the moment tB the coordinate of the point B is equal to xB,
(b) what time interval should separate the markings of coordinates of the rod's ends in the frame K for the difference of coordinates to become equal to the proper length of the rod.
View SolutionThe rod A′B′ moves with a constant velocity v relative to the rod AB (figure). Both rods have the same proper length l0 and at the ends of each of them clocks are mounted, which are synchronized pariwise: A with B and A′ with B′. Suppose the moment when the clock B′ gets opposite the clock A is taken for the beginning of the time count in the reference frames fixed to each of the rods. Determine:
(a) the readings of the clocks B and B′ at the moment when they are opposite each other,
(b) the same for the clocks A and A′.

View SolutionThe velocity components of a particle moving in the xy plane of the reference frame K are equal to vx and vy. Find the velocity v′ of this particle in the frame K in the positive direction of its x axis.
View SolutionA rod AB is moving on a fixed circle of radius R with constant velocity 'v' as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
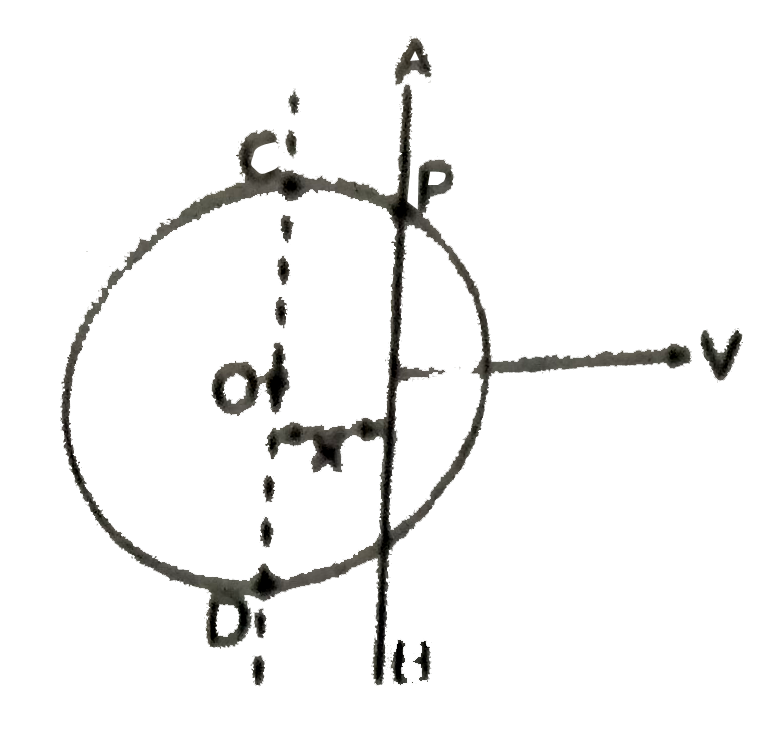
(a) Find the speed of point of intersection P
(b) Find the angular speed of point of intersection
P with respect to centre of the circle.
View Solution
