If two parallel lines are intersected by a transversal, prove that the bisectors of the two pairs of interior angles enclose a rectangle.
Step by step video & image solution for If two parallel lines are intersected by a transversal, prove that the bisectors of the two pairs of interior angles enclose a rectangle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINES AND ANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINES AND ANGLESEXERCISE - PART-D
8 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - PRACTICE TEST
12 Videos
- NUMBER SYSTEMSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - NUMBER SYSTEMSEXERCISE - Part - D
18 Videos
Similar Questions
Knowledge Check
If two parallel lines are intersected by a transversal , then the interior angles on the same side of the transversal are -
AequalBadjacentCSupplementaryDComplementaryTwo parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
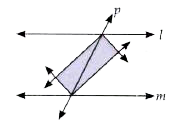 ATrapeziumBKiteCParallelogramDSquare
ATrapeziumBKiteCParallelogramDSquareIf two lines are intersected by a transversal, then the number of pairs of interior angles on the same side of the transversal is
A1B2C3D4
If two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIf two lines are intersected by a transversal; the bisectors of any pair of alternate interior angles are parallel.
View SolutionIf two parallel lines are intersected by a transversal; the bisector of any two corresponding angles are parallel.
View SolutionAB,CD are two parallel lines and a transversal l intersects AB at X and CD at Y Prove that the bisectors of the interior angles form a parallelogram, with all its angles right angles i.e., it is a rectangle.
View Solution
