In a parallelograms PQRS, M and N are points on PQ and RS such that PM = RN. Prove that MS || NQ.
The correct Answer is:Prove
To prove that MS∥NQ in the parallelogram PQRS where PM=RN, we will follow these steps:
Step 1: Understand the Given Information
We have a parallelogram PQRS with points M on PQ and N on RS such that PM=RN.
Hint: Identify the properties of a parallelogram, particularly that opposite sides are equal and parallel.
Step 2: Assign Lengths
Let PM=RN=x. Since PQRS is a parallelogram, the lengths of opposite sides are equal. Let PQ=RS=L.
Hint: Use variables to represent lengths to simplify calculations.
Step 3: Calculate Remaining Lengths
Now, we can find the lengths of MQ and NS:
- MQ=PQ−PM=L−x
- NS=RS−RN=L−x
Hint: Use the property of segments to express the remaining lengths in terms of the total length and the known segment.
Step 4: Establish Equality of Segments
From the calculations, we have:
- MQ=L−x
- NS=L−x
Thus, MQ=NS.
Hint: Note that if two segments are equal, they can be used to show parallelism in the next steps.
Step 5: Use the Parallelogram Properties
In the quadrilateral MQNS:
- We have MQ=NS (opposite sides are equal).
- We know PQ∥RS (as they are opposite sides of the parallelogram).
Hint: Recall the condition for a quadrilateral to be a parallelogram: if one pair of opposite sides is both equal and parallel, then the quadrilateral is a parallelogram.
Step 6: Conclude that MQNS is a Parallelogram
Since MQ=NS and PQ∥RS, by the properties of parallelograms, MQNS is a parallelogram.
Hint: Use the definition of a parallelogram to conclude that if one pair of opposite sides is both equal and parallel, the shape is a parallelogram.
Step 7: Prove MS∥NQ
In parallelogram MQNS, the opposite sides MS and NQ are parallel by definition.
Hint: Remember that in any parallelogram, opposite sides are always parallel.
Conclusion
Thus, we have proved that MS∥NQ.
We have a parallelogram PQRS with points M on PQ and N on RS such that PM=RN.
Let PM=RN=x. Since PQRS is a parallelogram, the lengths of opposite sides are equal. Let PQ=RS=L.
Now, we can find the lengths of MQ and NS:
- MQ=PQ−PM=L−x
- NS=RS−RN=L−x
From the calculations, we have:
- MQ=L−x
- NS=L−x
In the quadrilateral MQNS:
- We have MQ=NS (opposite sides are equal).
- We know PQ∥RS (as they are opposite sides of the parallelogram).
Since MQ=NS and PQ∥RS, by the properties of parallelograms, MQNS is a parallelogram.
In parallelogram MQNS, the opposite sides MS and NQ are parallel by definition.
Thus, we have proved that MS∥NQ.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - QUARILATERAL EXERCISE - Part - D5videos
QUARILATERAL
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - QUARILATERAL EXERCISE - Part - B12videos
QUARILATERAL
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROBABILITY MIND MAPEXERCISE - PRACTICE TEST6videos
PROBABILITY MIND MAP
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - PRACTICE TEST5videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
In △PQR, M and N are points on PQ and PR, respectively, such that ¯¯¯¯¯¯¯¯MN∣∣¯¯¯¯¯¯QR, If PM =x, PR =x+9,PQ=x+13 and PN=x−2, then find x.
A10B11C13D15 - Question 2 - Select One
In a ΔPQR, points M and N are on the sides PQ and PR respectively such that PM 0.6. PQ and NR=0.4PR. What percentage of the area of the triangle PQR does that of triangle PMN form?
AA)60%BB)50%CC)36%DD)55% - Question 3 - Select One
In a ΔPQR, points M and N are on the sides PQ and PR respectively such that PM 0.6. PQ and NR=0.4PR. What percentage of the area of the triangle PQR does that of triangle PMN form?
A60%B50%C36%D55%
In the figure, PSDA is a parallelogram. Points Q and R are taken on PS such that PQ=QR=RS and PA||QB||RC. Prove that ar(PQE)=ar(CFD).
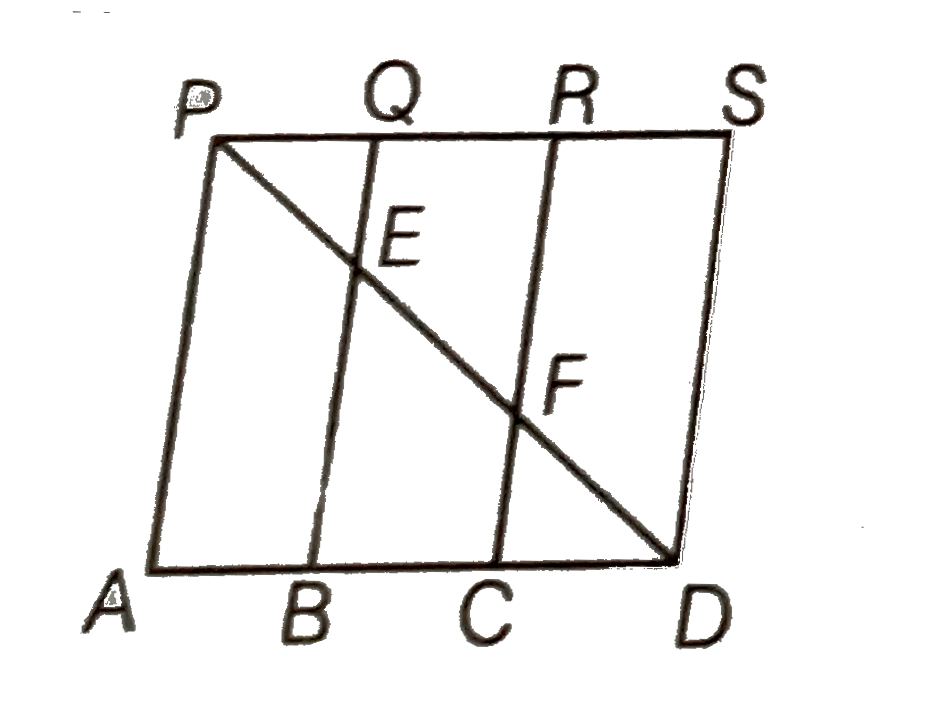 View Solution
View SolutionIn the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.
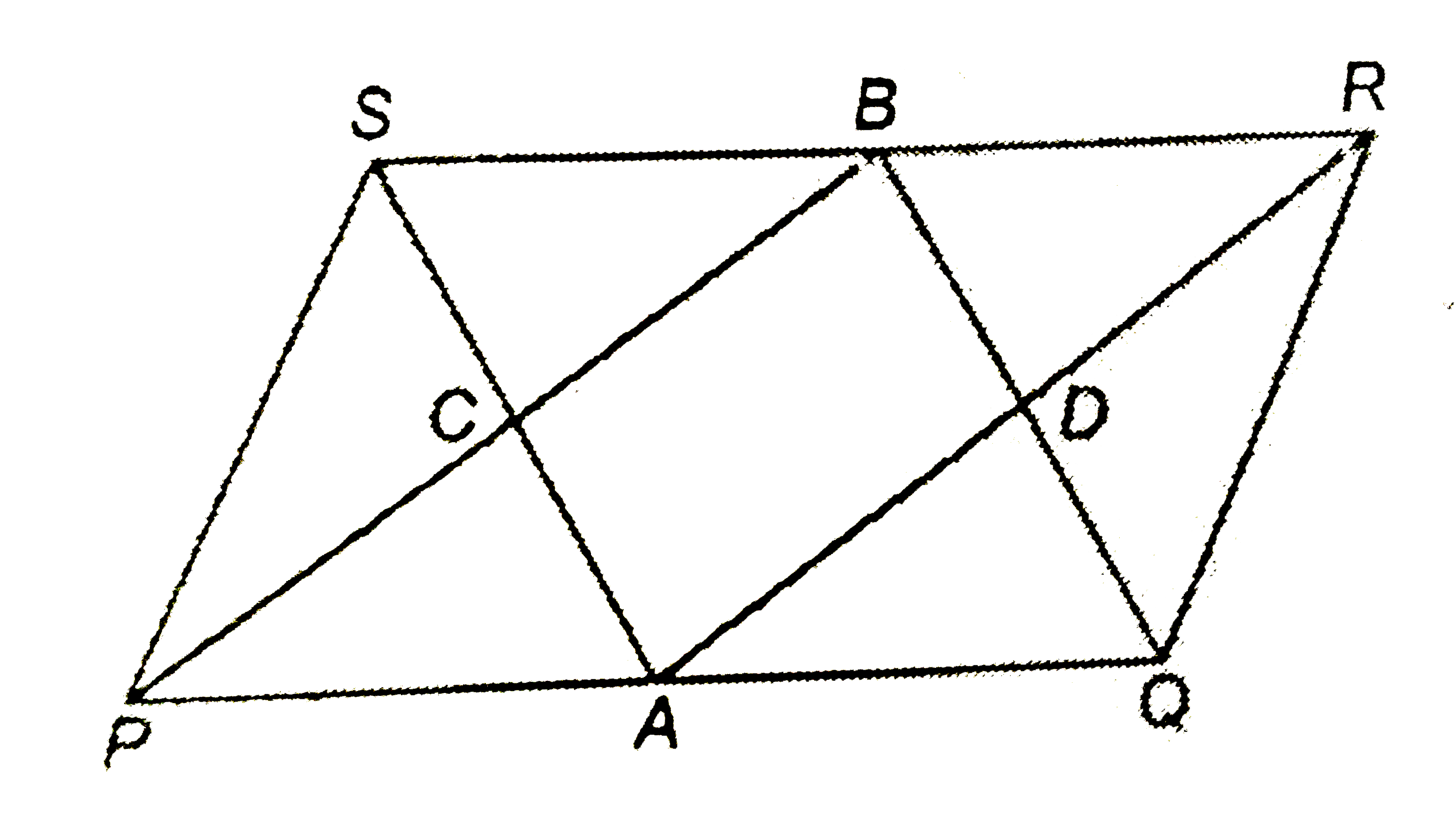 View Solution
View SolutionPQR is a triangle right-angled at P and M is a point on QR such that PM⊥QR. Show thatPM2=QM.MR.
View SolutionIn △PQR L and M are two points on the sides PQ and PR respectively such that LMII QR. If PL = 2cm, LQ = 6 cm and PM= 1.5 cm, then MR (in cm) is
View SolutionThe area of a parallelogram PQRS is 36cm2. M is any point on the side RS. The area of ΔPMQ is.
View Solution

