ABCD is a parallelogram. Side AB is produced on both sides to E & F as in figure such that BE = BC & AF = AD. Show that EC & FD when produced meets at right angle.
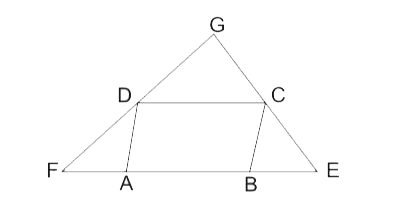
The correct Answer is:Prove
Step by step video, text & image solution for ABCD is a parallelogram. Side AB is produced on both sides to E & F as in figure such that BE = BC & AF = AD. Show that EC & FD when produced meets at right angle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - QUARILATERAL EXERCISE - Part - C10videos
QUARILATERAL
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - PROBABILITY MIND MAPEXERCISE - PRACTICE TEST6videos
PROBABILITY MIND MAP
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - PRACTICE TEST5videos
STATISTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AA)AN=√3ABBB)AN=2ABCC)AN2=32AB2DD)AN2=2AB2 - Question 2 - Select One
In a parallelogram ABCD, a side AB is extended to E such that BE = AB. If DE cut the line BC at Q then point Q divide BC in what ratio?
A1:2B1:1C2:3D2:1 - Question 3 - Select One
ABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
AAN=√3ABBAN=2ABCAN2=32AB2DAN2=2AB2
ABCD is a parallelogram. The circle through A,B and intersects CD produced at E. show that AD =AE.
View SolutionThe side AD of parallelogram ABCD is produced to a point E. BE intersects CD at F. Show that ΔABE~ΔCFB.
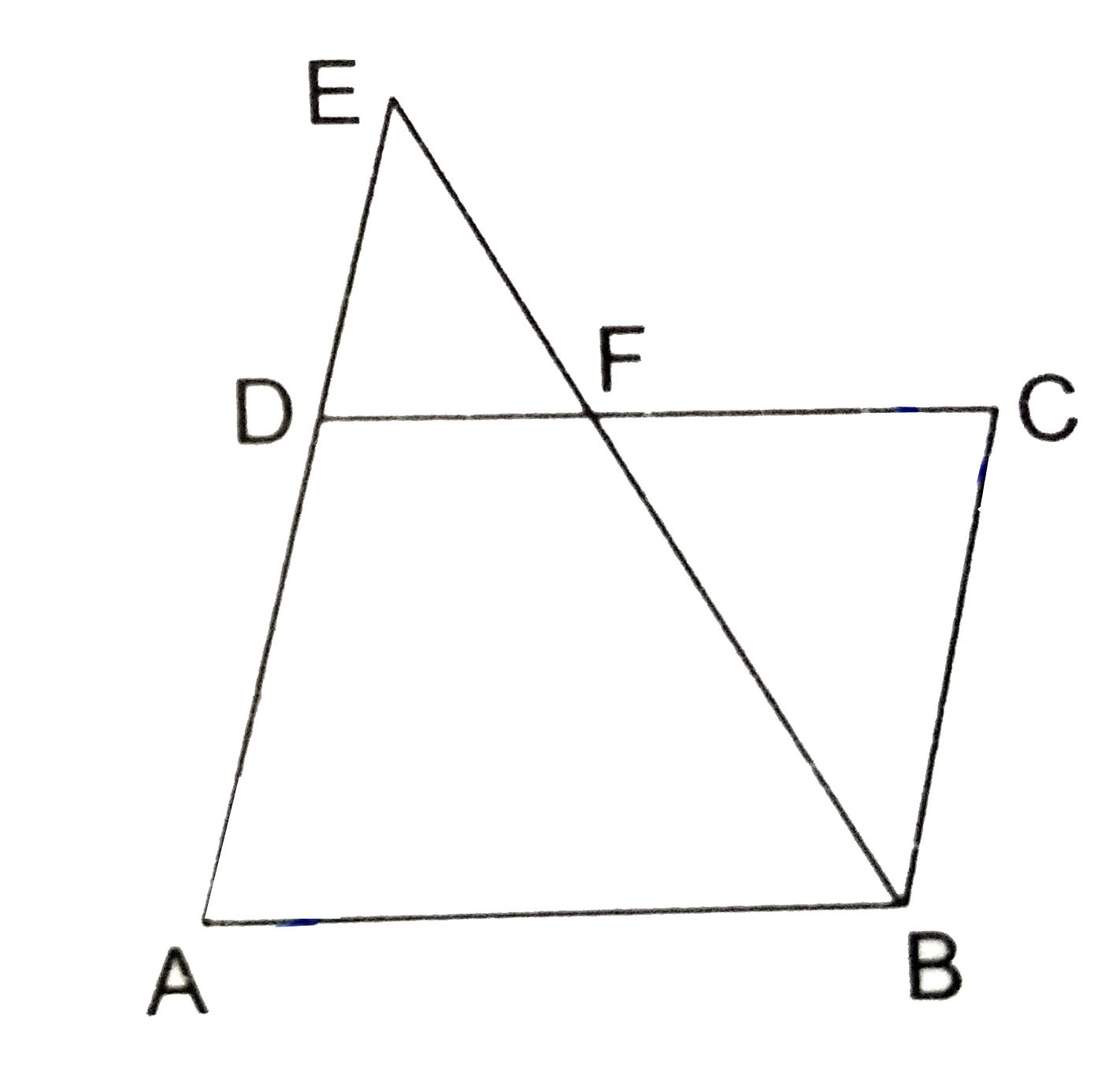 View Solution
View SolutionIn the figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(ΔBPC) = ar(ΔDPQ).
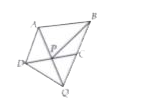 View Solution
View SolutionABCD is cyclic quadrilateral. Sides AB and DC, when produced meet at the point P and sides AD and BC, when produced meet at the point Q. If ∠ADC=85∘and∠BPC=40∘, then ∠CQD is equal to
View SolutionA dog takes 3 leaps for every 5 leaps of a hare. If one leap of the dog is equal to 3 leaps of the hare, the ratio of the speed of the dog to that of the hare is :
View Solution

