ABCD is cyclic quadrilateral. Sides AB and DC, when produced meet at the point P and sides AD and BC, when produced meet at the point Q. If ∠ADC=85∘and∠BPC=40∘, then ∠CQD is equal to
30∘
40∘
55∘
85∘
The correct Answer is:A
To solve the problem, we need to find the measure of angle CQD in the cyclic quadrilateral ABCD, given the angles ADC = 85° and BPC = 40°.
1. Understand the Properties of Cyclic Quadrilaterals:
In a cyclic quadrilateral, the sum of the opposite angles is supplementary. That means:
∠A+∠C=180∘and∠B+∠D=180∘
2. Identify the Angles:
We know:
- ∠ADC=85∘
- ∠BPC=40∘
3. Find Angle CDQ:
Since ADQ is a straight line, we can use the linear angle property:
∠ADC+∠CDQ=180∘
Substituting the known value:
85∘+∠CDQ=180∘
Therefore:
∠CDQ=180∘−85∘=95∘
4. Find Angle ABC:
Again using the property of cyclic quadrilaterals:
∠ABC+∠ADC=180∘
Thus:
∠ABC=180∘−85∘=95∘
5. Find Angle PCB:
In triangle PBC, we apply the angle sum property:
∠BPC+∠ABC+∠PCB=180∘
Substituting the known values:
40∘+95∘+∠PCB=180∘
Therefore:
∠PCB=180∘−135∘=45∘
6. Find Angle QDC:
Using the linear angle property again:
∠BPC+∠QDC=180∘
Thus:
40∘+∠QDC=180∘
Therefore:
∠QDC=180∘−40∘=140∘
7. Find Angle CQT:
In triangle CDQ, we apply the angle sum property:
∠CQD+∠QDC+∠QCD=180∘
We already found:
- ∠QDC=95∘
- ∠QCD=45∘
Thus:
∠CQD+95∘+45∘=180∘
Therefore:
∠CQD=180∘−140∘=40∘
Final Answer:
∠CQD=40∘
In a cyclic quadrilateral, the sum of the opposite angles is supplementary. That means:
∠A+∠C=180∘and∠B+∠D=180∘
We know:
- ∠ADC=85∘
- ∠BPC=40∘
Since ADQ is a straight line, we can use the linear angle property:
∠ADC+∠CDQ=180∘
Substituting the known value:
85∘+∠CDQ=180∘
Therefore:
∠CDQ=180∘−85∘=95∘
Again using the property of cyclic quadrilaterals:
∠ABC+∠ADC=180∘
Thus:
∠ABC=180∘−85∘=95∘
In triangle PBC, we apply the angle sum property:
∠BPC+∠ABC+∠PCB=180∘
Substituting the known values:
40∘+95∘+∠PCB=180∘
Therefore:
∠PCB=180∘−135∘=45∘
Using the linear angle property again:
∠BPC+∠QDC=180∘
Thus:
40∘+∠QDC=180∘
Therefore:
∠QDC=180∘−40∘=140∘
In triangle CDQ, we apply the angle sum property:
∠CQD+∠QDC+∠QCD=180∘
We already found:
- ∠QDC=95∘
- ∠QCD=45∘
Thus:
∠CQD+95∘+45∘=180∘
Therefore:
∠CQD=180∘−140∘=40∘
∠CQD=40∘
Topper's Solved these Questions
- BOOK - LUCENT PUBLICATIONCHAPTER - CIRCLE AND ITS TANGENT LINESEXERCISE - EXERCISE 8A71videos
CIRCLE AND ITS TANGENT LINES
- BOOK - LUCENT PUBLICATIONCHAPTER - CENTRE OF TRIANGLEEXERCISE - EXERCISE-6B8videos
CENTRE OF TRIANGLE
- BOOK - LUCENT PUBLICATIONCHAPTER - CONGRUENCE AND SIMILAR TRIANGLES EXERCISE - EXERCISE-5B8videos
CONGRUENCE AND SIMILAR TRIANGLES
Similar Questions
If ABCD is circular quadrilateral. If side AB and DC meets at point P on extension similarly AD and BC meet at point Q. If ∠ADC=85,∠BPC=40∘, find ∠CQD.
View SolutionABCD is a cyclic quadrilateral such that its sides AD and BC produced meet at P and sides AB and DC produced meet at Q. If ∠A=62∘ and ∠ABC=74∘, then the difference between ∠P and ∠Q is:
ABCD एक चक्रीय चतुर्भुज है जो इस प्रकार है कि इसकी भुजाओं AD और BC को बढ़ाने पर वे P पर मिलती हैं तथा AB और DC को बढ़ाने पर वे Q पर मिलती हैं | यदि ∠=62∘ और ∠ABC=74∘ है, तो ∠P और ∠Q के बीच अंतर ज्ञात करें |View Solution
Knowledge Check
- Question 1 - Select One
A dog takes 3 leaps for every 5 leaps of a hare. If one leap of the dog is equal to 3 leaps of the hare, the ratio of the speed of the dog to that of the hare is :
AA) 9:5BB) 2:3CC) 4:7DD) 5:6 - Question 2 - Select One
The sides AB and CD of a cyclic quadrilateral ABCD are produced to meet at P. The sides AD and BC are produced to meet at Q. If ∠ADC=85∘and∠BPC=40∘, then ∠BAD is equal to
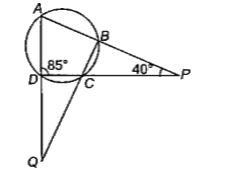 A45∘B30∘C95∘D55∘
A45∘B30∘C95∘D55∘ - Question 3 - Select One
ABCD is cyclic quadrilateral. Sides AB and DC, when produced , meet at E and sides BC and AD, when produced, meet at F. If ∠BFA=60∘ and ∠AED=30∘ , then the measure of ∠ABC is :
AA)75∘BB)65∘CC)80∘DD)70∘
ABCD is a cyclic quadrilateral such that its sides AD and BD produced meet at P and sides AB and DC produced meet at Q. If ∠A=62∘ and ∠ABC=74∘ then the difference between ∠P and ∠Q is :
ABCD एक चक्रीय चतुर्भज है, जिसकी भुजाएं AD और BCबढ़कर बिंदु P पर मिलती है और भुजा AB और DCबढ़कर बिंदु Q पर मिलती है| यदि ∠A=62∘ और ∠ABC=74∘ है तो ∠P और ∠Q के बीच का अंतर हैःView SolutionABCD is a cyclic quadrilateral in which sides AD and BC are produced to meet at P, and sides DC and AB meet at Q when produced. If ∠A=60∘ and ∠ABC=72∘ then ∠DPC−∠BQC=
ABCD एक चक्रीय चतुर्भुज है जिसमें भुजाओं AD तथा BC को बढ़ाया जाता है जो P पर मिलती हैं तथा भुजाओं DC और AB को बढ़ाया जाता है जो Q पर मिलती हैं | यदि ∠A=60∘ तथा ∠ABC=72∘ है, तो ∠DPC−∠BQC= ?View SolutionABCD is a cyclic quadrilateral in which sides AD and BC are produced to meet at P, and sides DC and AB meet at Q when produced. If ∠A=60∘ and ∠ABC=72∘ then ∠DPC−∠BQC=
ABCD एक चक्रीय चतुर्भुज है जिसमें भुजाओं AD तथा BC को बढ़ाया जाता है जो P पर मिलती हैं तथा भुजाओं DC और AB को बढ़ाया जाता है जो Q पर मिलती हैं | यदि ∠A=60∘ तथा ∠ABC=72∘ है, तो ∠DPC−∠BQC= ?View SolutionThe sides AB and CD of a cyclic quadrilateral ABCD are produced to meet at P. The sides AD and BC are produced to meet at P. The sides AD and BC are produced to meet at Q. If <ADC=85∘ and <BPC=40∘, then <BAD is equal to
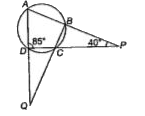 View Solution
View SolutionSides AB and DC of a cyclic quadrilateral ABCD are produced to meet at E, and sides AD and BC are produced to meet at F. If ∠ADC=75∘ and ∠BEC=52∘, then the difference between ∠BAD and ∠AFB ? /
एक चक्रीय चतुर्भुज ABCD की भुजाओं AB और DC को बढ़ाया जाता है जो E पर मिलती हैं तथा भुजाओं AD और BC को बढ़ाया जाता है जो F पर मिलती हैं | यदि ∠ADC=75∘ तथा ∠BEC=52∘ हैं, तो ∠BAD तथा ∠AFB के बीच क्या अंतर है?View Solution

