TP and TQ are the tangents from the external point T of a circle with centre O. If ∠OPQ=30∘ then find the measure of ∠TQP.
The correct Answer is:60∘
To solve the problem, we need to find the measure of angle TQP given that angle OPQ is 30 degrees. Here’s how we can approach the solution step by step:
Step 1: Understand the Geometry
We have a circle with center O, and two tangents TP and TQ drawn from an external point T to points P and Q on the circle. By the properties of tangents, we know that OP and OQ are radii of the circle.
Step 2: Identify Given Angles
We are given that angle OPQ = 30 degrees.
Step 3: Identify Right Angles
Since OP and OQ are radii and TP and TQ are tangents, we know that:
- Angle OTP = 90 degrees (tangent to radius)
- Angle OTQ = 90 degrees (tangent to radius)
Step 4: Use the Triangle Properties
In triangle OPQ, we can find angle OQT:
- Angle OPT + angle OPQ + angle OQP = 180 degrees (sum of angles in a triangle)
- We know angle OPT = 90 degrees and angle OPQ = 30 degrees.
So, we can write:
90+30+angle OQP=180
This simplifies to:
angle OQP=180−120=60 degrees
Step 5: Relate Angles in Triangle TQP
Now, we need to find angle TQP. Since TP = TQ (tangents from the same external point), triangle TQP is isosceles. Therefore:
- Angle TQP = angle QTP.
Step 6: Use the Angle Sum Property
In triangle TQP:
- Angle TQP + angle QTP + angle QPT = 180 degrees.
Since angle QPT = angle OQP = 60 degrees, we have:
angle TQP+angle TQP+60=180
Let angle TQP = x:
x+x+60=180
This simplifies to:
2x+60=180
Subtracting 60 from both sides gives:
2x=120
Dividing by 2 gives:
x=60
Conclusion
Thus, the measure of angle TQP is 60 degrees.
We have a circle with center O, and two tangents TP and TQ drawn from an external point T to points P and Q on the circle. By the properties of tangents, we know that OP and OQ are radii of the circle.
We are given that angle OPQ = 30 degrees.
Since OP and OQ are radii and TP and TQ are tangents, we know that:
- Angle OTP = 90 degrees (tangent to radius)
- Angle OTQ = 90 degrees (tangent to radius)
In triangle OPQ, we can find angle OQT:
- Angle OPT + angle OPQ + angle OQP = 180 degrees (sum of angles in a triangle)
- We know angle OPT = 90 degrees and angle OPQ = 30 degrees.
90+30+angle OQP=180
This simplifies to:
angle OQP=180−120=60 degrees
Now, we need to find angle TQP. Since TP = TQ (tangents from the same external point), triangle TQP is isosceles. Therefore:
- Angle TQP = angle QTP.
In triangle TQP:
- Angle TQP + angle QTP + angle QPT = 180 degrees.
angle TQP+angle TQP+60=180
Let angle TQP = x:
x+x+60=180
This simplifies to:
2x+60=180
Subtracting 60 from both sides gives:
2x=120
Dividing by 2 gives:
x=60
Thus, the measure of angle TQP is 60 degrees.
Topper's Solved these Questions
- CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - SHORT ANSWER TYPE - II QUESTIONS
4 Videos
- CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - LONG ANSWER TYPE QUESTIONS
2 Videos
- CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PRACTICE - TEST (SECTION - D)
1 Videos
- ARITHMETIC PROGRESSION BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - ARITHMETIC PROGRESSION EXERCISE - PRACTICE TEST (SECTION D)
1 Videos
- Co-ordinate GeometryBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - Co-ordinate GeometryEXERCISE - PRACTICE-TEST (Coordinate Geometry) SECTION-D
1 Videos
Similar Questions
In the figure, PA is a tangent from an external point P to the circle with centre O and diameter AB. If ∠POB=110∘, then the measure of ∠APO is:
View SolutionIn the given figure, TP and TQ are tangents drawn from an external point T to a circle with centre O such that ∠TQP=60∘. Find angelOPQ.
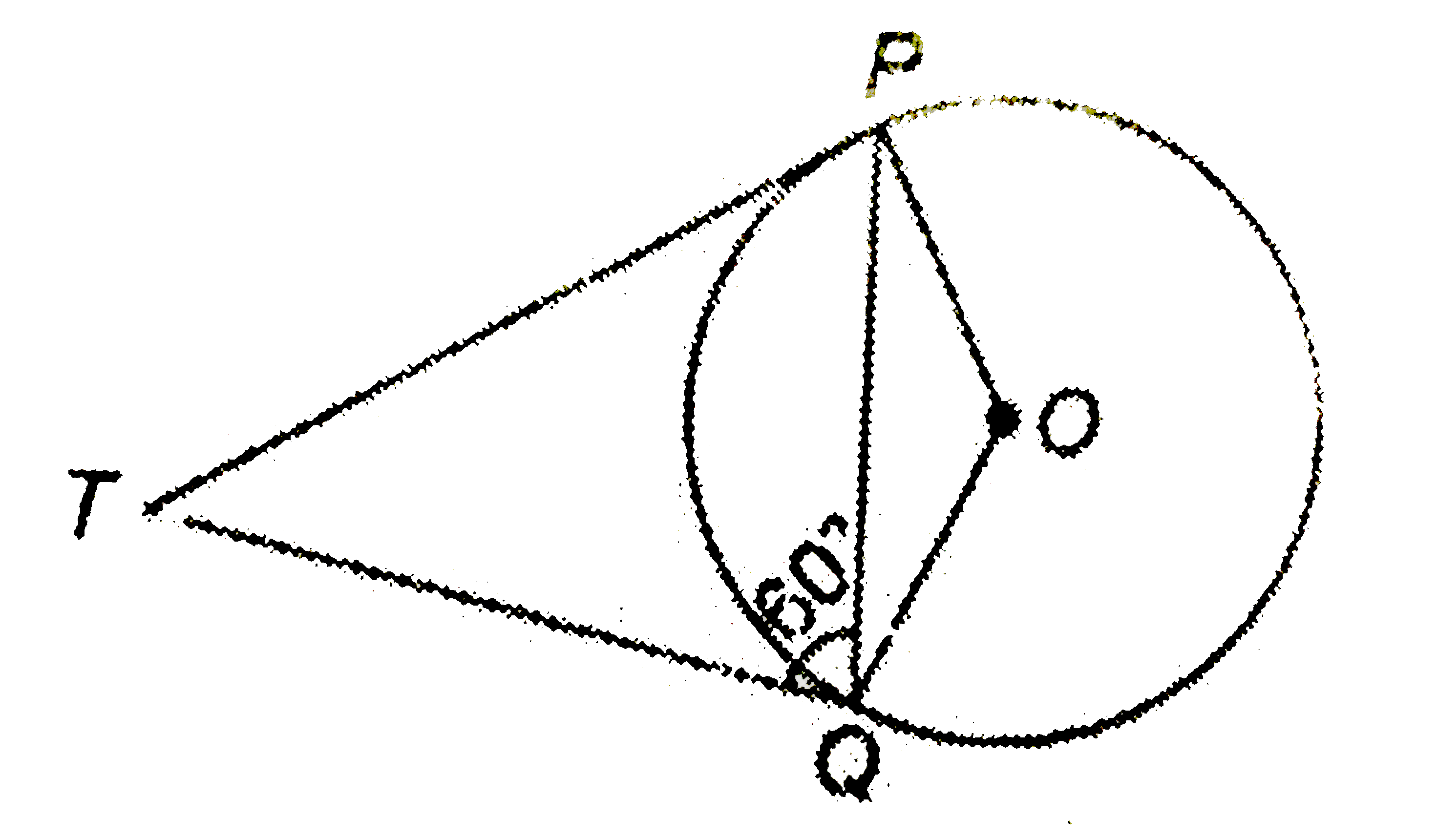
View Solution
Knowledge Check
In the figure, PA is a tangent from an external point P to the circle with centre O and diameter AB. If ∠POB=110∘, then the measure of ∠APO is:
A40∘B20∘C25∘D30∘In the figure , if TP and TQ are tangents drawn from an external point T to a circle with centre O such that ∠TQP=60∘, then ∠OPQ =
 A25∘B60∘C40∘D30∘
A25∘B60∘C40∘D30∘In the figure , PQ and PR are the tangents drawn form P to a circle with centre O. if ∠OPQ=35∘ then
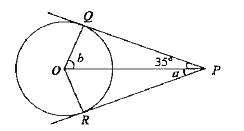 Aa=30∘,b=60∘Ba=35∘,b=55∘Ca=40∘,b=50∘Da=45∘,b=45∘
Aa=30∘,b=60∘Ba=35∘,b=55∘Ca=40∘,b=50∘Da=45∘,b=45∘
In the figure, PA is a tangent from an external point P to a circle with centre O. If ∠POB=115∘, find ∠APO.

View SolutionFrom the external point P tangents PA and PB are drawn to a circle with centre O. If ∠PAB=50∘, then find ∠AOB.
View SolutionIn figure , APB is a tangent to a circle with centre O at point, If ∠QPB=50∘ , then the measure of ∠POQ is
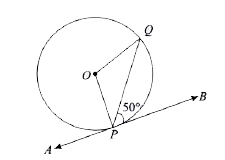
View SolutionIn the given figure, AP and BP are tangents to a circle with centre O. IF ∠APB=62∘ then the measure of ∠AQB is

View SolutionIn the figure, TP and TQ are tangents drawn to the circle with centre at O. If ∠POQ=115∘ then ∠PTQ is:
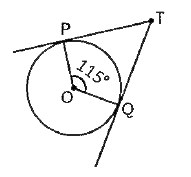
View Solution
