In the figure, PA is a tangent from an external point P to the circle with centre O and diameter AB. If ∠POB=110∘, then the measure of ∠APO is:
a)30∘
b)40∘
c)25∘
d)20∘
To solve the problem step by step, we will use the properties of tangents and angles in a circle.
Step 1: Understand the given information
We have a circle with center O and diameter AB. PA is a tangent to the circle at point A, and we are given that the angle POB is 110 degrees.
Hint: Remember that a tangent to a circle forms a right angle with the radius at the point of tangency.
Step 2: Identify the angles
Since PA is a tangent to the circle at point A, we know that the angle OAP (the angle between the radius OA and the tangent PA) is 90 degrees.
Hint: Use the property that the radius at the point of tangency is perpendicular to the tangent line.
Step 3: Use the linear pair property
The angles POB and POA form a linear pair, which means they add up to 180 degrees. Therefore, we can find angle POA:
Angle POA=180∘−Angle POB=180∘−110∘=70∘
Hint: Linear pairs of angles always sum to 180 degrees.
Step 4: Set up the triangle
Now, we have triangle APO. The angles in triangle APO are:
- Angle APO (which we want to find)
- Angle POA (which we found to be 70 degrees)
- Angle OAP (which is 90 degrees)
Step 5: Apply the angle sum property of triangles
According to the angle sum property of triangles, the sum of the angles in triangle APO is 180 degrees:
Angle APO+Angle POA+Angle OAP=180∘
Substituting the known values:
Angle APO+70∘+90∘=180∘
Step 6: Solve for angle APO
Now, simplify the equation:
Angle APO+160∘=180∘
Subtract 160 degrees from both sides:
Angle APO=180∘−160∘=20∘
Conclusion
Thus, the measure of angle APO is 20 degrees.
Final Answer: Angle APO = 20 degrees.
---
We have a circle with center O and diameter AB. PA is a tangent to the circle at point A, and we are given that the angle POB is 110 degrees.
Since PA is a tangent to the circle at point A, we know that the angle OAP (the angle between the radius OA and the tangent PA) is 90 degrees.
The angles POB and POA form a linear pair, which means they add up to 180 degrees. Therefore, we can find angle POA:
Now, we have triangle APO. The angles in triangle APO are:
- Angle APO (which we want to find)
- Angle POA (which we found to be 70 degrees)
- Angle OAP (which is 90 degrees)
According to the angle sum property of triangles, the sum of the angles in triangle APO is 180 degrees:
Now, simplify the equation:
Thus, the measure of angle APO is 20 degrees.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure, PA is a tangent from an external point P to the circle with centre O and diameter AB. If ∠POB=110∘, then the measure of ∠APO is:
A40∘B20∘C25∘D30∘In figure , APB is a tangent to a circle with centre O at point, If ∠QPB=50∘ , then the measure of ∠POQ is
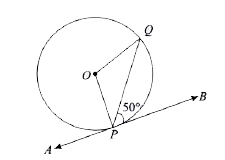 A100∘B120∘C140∘D150∘
A100∘B120∘C140∘D150∘In the figure , if TP and TQ are tangents drawn from an external point T to a circle with centre O such that ∠TQP=60∘, then ∠OPQ =
 A25∘B60∘C40∘D30∘
A25∘B60∘C40∘D30∘
PQ is a tangent drawn from an external point P to a circle with center O, ∠QOR is the diameter of the circle. If ∠POR=120∘. What is the measure of ∠OPQ?
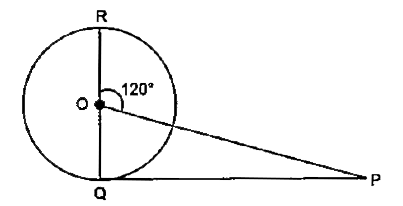
View SolutionIn figure PQ is a tangent at a point C to a circle with centre O. If AB is a diameter and ∠CAB=30∘, find ∠PCA
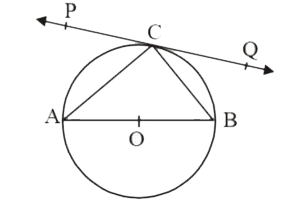
View SolutionPQ is a tangent at a point C to a circle with centre O if AB is a diameter and angle CAB=30∘, find angle PCA.
View SolutionIn the given figure, PQ is a tangent at a point R of the circle with centre O. If ∠TRQ=30∘, then ∠PRS is equal to
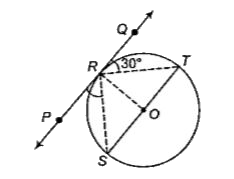
View SolutionIn the given figure, AP and BP are tangents to a circle with centre O. IF ∠APB=62∘ then the measure of ∠AQB is

View Solution

