If a is A.M. of b and c and c,G1,G2,b are in G.P., then find the value of G31+G32−2abc
To solve the problem, we need to find the value of G31+G32−2abc given that a is the arithmetic mean of b and c, and c,G1,G2,b are in geometric progression (G.P.).
1. Understanding the Arithmetic Mean:
Since a is the arithmetic mean of b and c, we can express this relationship as:
a=b+c2
Rearranging gives us:
b+c=2a
2. Setting Up the Geometric Progression:
Given that c,G1,G2,b are in G.P., we can denote the common ratio as r. Therefore, we can express G1 and G2 in terms of c and b:
G1=c⋅randG2=c⋅r2andb=c⋅r3
3. Finding the Common Ratio r:
From the expression for b:
r3=bc⟹r=(bc)1/3
4. Expressing G1 and G2:
Substituting for r:
G1=c⋅(bc)1/3=c2/3b1/3
G2=c⋅(bc)2/3=c1/3b2/3
5. Calculating G31+G32:
Now, we need to calculate G31+G32:
G31=(c2/3b1/3)3=c2b
G32=(c1/3b2/3)3=cb2
Therefore,
G31+G32=c2b+cb2
6. Factoring G31+G32:
We can factor this expression:
G31+G32=c(b+c)b
7. Substituting b+c:
From step 1, we know b+c=2a. Thus,
G31+G32=c(2a)b=2abc
8. Final Calculation:
Now we substitute back into the expression we need to evaluate:
G31+G32−2abc=2abc−2abc=0
Conclusion:
The value of G31+G32−2abc is:
0
Since a is the arithmetic mean of b and c, we can express this relationship as:
a=b+c2
Rearranging gives us:
b+c=2a
Given that c,G1,G2,b are in G.P., we can denote the common ratio as r. Therefore, we can express G1 and G2 in terms of c and b:
G1=c⋅randG2=c⋅r2andb=c⋅r3
From the expression for b:
r3=bc⟹r=(bc)1/3
Substituting for r:
G1=c⋅(bc)1/3=c2/3b1/3
G2=c⋅(bc)2/3=c1/3b2/3
Now, we need to calculate G31+G32:
G31=(c2/3b1/3)3=c2b
G32=(c1/3b2/3)3=cb2
Therefore,
G31+G32=c2b+cb2
We can factor this expression:
G31+G32=c(b+c)b
From step 1, we know b+c=2a. Thus,
G31+G32=c(2a)b=2abc
Now we substitute back into the expression we need to evaluate:
G31+G32−2abc=2abc−2abc=0
The value of G31+G32−2abc is:
0
Topper's Solved these Questions
- SEQUENCES AND SERIES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SEQUENCES AND SERIES EXERCISE - SECTION-C(SHORT anwer type )
34 Videos
- REALATION AND FUNCTIONS BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - REALATION AND FUNCTIONS EXERCISE - SHORT ANSWER TYPE QUESTIONS (4 MARKS)
29 Videos
- SETS AND FUNCTIONSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SETS AND FUNCTIONSEXERCISE - LONG ANSWER TYPE QUESTIONS
21 Videos
Similar Questions
If a.b.c are in G.P. then
View SolutionIf a,A1,A2,b are in A.P.,a,G1,G2,b are in G.P. and a,H1,H2,b are in H.P., then the value of G1G2(H1+H2)−H1H2(A1+A2) is
View Solution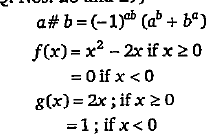
Find the value of f(g(2#3)+g(f(1#2) :
View SolutionIf a is the A.M. of bandc and the two geometric means are G1andG2 , then prove that G31+G32=2abc
View SolutionIf a is the A.M. of b and c and the two geometric mean are G1 and G2, then prove that G31+G32=2ab⋅
View SolutionIf a,b,c are in G.P. and b−c,c−a,a−b are in H.P. then find the value of (a+b+c)2b2 .
View SolutionIf a be one A.M and G1 and G2 be then geometric means between b and c then G31+G32=
View SolutionIf A1 ,be the A.M.and G1,G2 be two G.M.'s between two positive numbers then G31+G32G1G2A1 is equal to:
View SolutionIf A1 and A2 are two A.M.s between a and b and G1 and G2 are two G.M.s between the same numbers then what is the value of A1+A2G1G2
View SolutionLef a, b be two distinct positive numbers and A and G their arithmetic and geometric means respectively. If a, G1,G2, b are in G.P. and a, H1,H2, b are in H.P., prove that G1G2H1H2<A2G2.
View Solution
