c. The mean deviation about Median for 1, 3, 5, 7, 9 is 5.
To determine whether the statement "The mean deviation about the median for the data set 1, 3, 5, 7, 9 is 5" is correct, we will follow these steps:
Step 1: Identify the Observations
The given observations are:
1, 3, 5, 7, 9
Step 2: Calculate the Median
Since the number of observations (n) is odd (n = 5), the median can be found using the formula:
Median=n+12th term
Calculating this gives:
Median=5+12=3rd term
Looking at the ordered observations, the 3rd term is 5. Thus, the median is:
Median=5
Step 3: Calculate the Mean Deviation about the Median
The mean deviation about the median is calculated using the formula:
Mean Deviation=∑|xi−Median|n
Where xi are the observations and n is the total number of observations.
Step 4: Calculate the Absolute Deviations
Now we calculate the absolute deviations from the median (5):
- For x1=1: |1−5|=4
- For x2=3: |3−5|=2
- For x3=5: |5−5|=0
- For x4=7: |7−5|=2
- For x5=9: |9−5|=4
Step 5: Sum the Absolute Deviations
Now, we sum these absolute deviations:
∑|xi−Median|=4+2+0+2+4=12
Step 6: Calculate the Mean Deviation
Now, we divide the total absolute deviation by the number of observations (n = 5):
Mean Deviation=125=2.4
Conclusion
The calculated mean deviation about the median is 2.4, not 5. Therefore, the statement "The mean deviation about the median for 1, 3, 5, 7, 9 is 5" is incorrect.
Final Answer
The statement is wrong.
---
The given observations are:
1, 3, 5, 7, 9
Since the number of observations (n) is odd (n = 5), the median can be found using the formula:
Median=n+12th term
Calculating this gives:
Median=5+12=3rd term
Looking at the ordered observations, the 3rd term is 5. Thus, the median is:
Median=5
The mean deviation about the median is calculated using the formula:
Mean Deviation=∑|xi−Median|n
Where xi are the observations and n is the total number of observations.
Now we calculate the absolute deviations from the median (5):
- For x1=1: |1−5|=4
- For x2=3: |3−5|=2
- For x3=5: |5−5|=0
- For x4=7: |7−5|=2
- For x5=9: |9−5|=4
Now, we sum these absolute deviations:
∑|xi−Median|=4+2+0+2+4=12
Now, we divide the total absolute deviation by the number of observations (n = 5):
Mean Deviation=125=2.4
The calculated mean deviation about the median is 2.4, not 5. Therefore, the statement "The mean deviation about the median for 1, 3, 5, 7, 9 is 5" is incorrect.
The statement is wrong.
Topper's Solved these Questions
- STATISTICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - Section - B (Very Short Answer Type Questions) (2 Mark)
5 Videos
- STATISTICSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STATISTICSEXERCISE - Section - C (Long Answer Type-I Questions) (4 Mark)
10 Videos
- SETS AND FUNCTIONSBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SETS AND FUNCTIONSEXERCISE - LONG ANSWER TYPE QUESTIONS
21 Videos
- STRAIGHT LINES BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - STRAIGHT LINES EXERCISE - SECTION-D (LONG ANSWER TYPE QUESTIONS )
23 Videos
Similar Questions
Knowledge Check
What is the mean deviation about the mean for the data 4, 7, 8, 9, 10, 12, 13, 17?
A2.5B3C3.5D4What is the mean deviation about the mean for the data 4, 7, 8, 9, 10, 12, 13 and 17?
A2.5B3C3.25D4The mean deviation of the data 3, 10, 10, 4, 7, 10, 5 is
A497B197C507D187
Find the mean deviation using median:
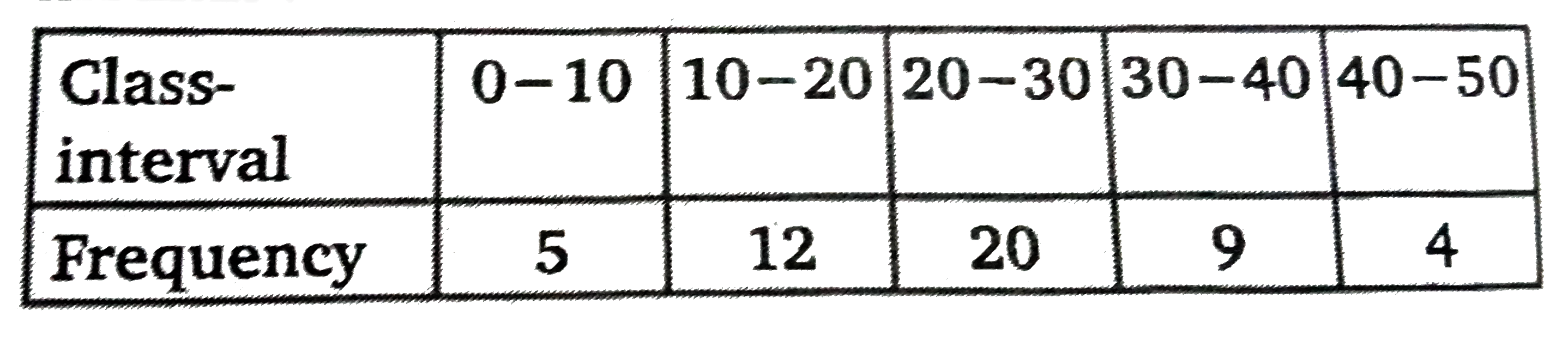
View SolutionThe mean deviation about the median of the numbers 2, 3, 5, 20, 17, 15, 11, 9, 7 is
View SolutionFind the mean deviation about the median for the data : xi 15 21 27 30 35 fi 3 5 6 7 8
View SolutionFind the mean deviation about the median for the data : xi: 5 7 9 10 12 15. fi: 8 6 2 2 2 6
View SolutionIf mean deviations about median of x,2x,3x,4x,5x,6x,7x,8x,9x,10x is 30, then |x| equals:-
View Solution
