Deduce the expression, N=N−λt0e, for the law of radioactive decay.
Radioactive decay Law: The rate of decay of radioactive nuclei is directly proportional to the number of undecayed nuclei at that time.
Derivation of Formula Suppose initially the number of atoms in radioactive element is No and N the number of atoms after time t.
After time t, let dN be the number of atoms which disintegrate in a short interval dt, then rate of disintegration will be dNdt, this is also called the activity of the substance/element.
According to Rutherford-Soddy law
dNdt,αN
or dNdt,=−λN ..(i)
where λ is a constant, called decay constant or disintegration constant of the element. Its unit is s–1. Negative sign shows that the rate of disintegration decreases with increase of time. For a given element/substance λ is a constant and is different for different elements. Equation (i) may be rewritten as
dNN=(−λdt)
Integrating loge,N=−λt+C...(ii )
where C is a constant of integration.
At t=0,N=N0
∴logeN0=0+C⋅⋅C=logeN0
∴ Equation (ii) gives logeN=−λt+logeN0
or logeN−logeN0=−λt
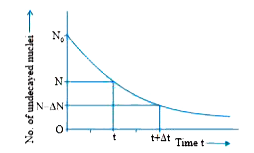
According to this equation, the number of undecayed atoms/nuclei of a given radioactive element decreases exponentially with time (i.e., more rapidly at first and slowly afterwards).
Mark of N=N016 in terms of T1/2 is shown in fig.
Topper's Solved these Questions
- CBSE Examination Paper Delhi–2014BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE Examination Paper Delhi–2014EXERCISE - Set-II (Questions Uncommon to Set-I)
10 Videos
- CBSE Examination Paper Delhi–2014BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE Examination Paper Delhi–2014EXERCISE - SET-III (Questions Uncommon to set-I and II)
9 Videos
- CBSE EXAMINATION PAPER - 2016 BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE EXAMINATION PAPER - 2016 EXERCISE - SECTION - E
17 Videos
- CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)EXERCISE - SECTION E
6 Videos
Similar Questions
(a) Deduce the expression, N=N0e−λt for the law of radioactive decay.
(b) (i) Write symbolically the process expressing the β+ decay of 2211Na. Also write the basic nuclear process underlying this decay.
(ii) Is the nucleus formed in the decay of the nucleus 2211Na, an isotope or isobar ?
View SolutionDeduce the expression, N=N−λt0 for the law of radioactive decay.
(b) Is the nucleus formed in the decay of the nucleus .1211Na, an isotope or isobar?
View Solution
Knowledge Check
Radioactive decay follows first-order kinetic. The mean life and half-life of nuclear decay process are τ=1/λ and t1/2=0.693/λ. Therefore are a number of radioactive elements in nature, their abundance is directly proportional to half life. The amount remaining after n half lives of radioactive elements can be calculated using the relation:
N=N0(12)n
The rate of radioactive decay isAIndependent of limeBIndependent of temperatureCDependent on catalystDDependent on the amount of elementsd not yet decayedThe mathematical equation of law of radioactive decay is
AN=N0e−λtBN=e−λtCN=N0eλtDN0=Ne−λtRadioactive disintergation always follow I order kinetics and is independent of all external factors and is represented by the relation N=N0e−λt where λ is decay constant and N atoms are left at time t. The radioactive nature of element is expressed in terms of average life numerically equal to decay constant (1/λ) however all the radioactive do not lose their radioactive nature in thier average life. The radioactive emission involves α,β particles as well as γ− rays.The penertrating power order is α<β<γ. The emissions can perntrate even thick steel walls but are however unable to penttrate Pb blocks. The S unit fo rate of decay is dps.
The percentage of atoms decayed in average life of a radioactive element is:A36.78%B63.22%C3.678%D6.322%
Radioactive Decay Law
View SolutionDerive the relation Nt=N0e−λt for radioactive decay. Obtain the relation between disintegration constant and half-life.
View SolutionWhat is radioactivity ? Derive an experssion N=N0e−λt for radioactive disintegration.
View SolutionExpand the following N=N0e−λt
View SolutionStability Curve and Laws of Radioactive Decay
View Solution