Does a charge Particle gain K.E. when passed through magnetic field region? Justify.
To determine whether a charged particle gains kinetic energy when it passes through a magnetic field, we can analyze the situation step by step.
1. Understanding the Scenario:
- We have a charged particle (with charge q) moving with an initial velocity v and enters a region with a uniform magnetic field B.
2. Direction of Motion and Magnetic Field:
- Assume the particle is moving in a direction perpendicular to the magnetic field. For example, if the particle moves in the positive x-direction, the magnetic field can be directed in the negative z-direction.
3. Applying Lorentz Force:
- The force acting on the charged particle due to the magnetic field is given by the Lorentz force formula:
F=q(v×B)
- Since the velocity v and the magnetic field B are perpendicular, the magnitude of the force can be expressed as:
F=qvB
4. Effect of the Magnetic Force:
- The magnetic force acts perpendicular to the velocity of the charged particle. This means that while the particle's direction changes, the speed (magnitude of velocity) remains constant.
5. Circular Motion:
- The perpendicular force causes the particle to undergo circular motion. In uniform circular motion, the speed of the particle does not change, only its direction does.
6. Kinetic Energy Calculation:
- The kinetic energy KE of the particle is given by:
KE=12mv2
- Since the speed v of the particle remains constant while it is in the magnetic field, the kinetic energy also remains constant.
7. Work-Energy Theorem:
- According to the work-energy theorem, the work done on the particle is equal to the change in kinetic energy. Since the magnetic force is always perpendicular to the displacement of the particle, the work done by the magnetic force is zero:
W=F⋅d⋅cos(90∘)=0
- Therefore, the change in kinetic energy is also zero:
KEfinal−KEinitial=0
8. Conclusion:
- Since there is no change in kinetic energy, we conclude that a charged particle does not gain kinetic energy when it passes through a magnetic field region.
Final Answer:
No, a charged particle does not gain kinetic energy when passed through a magnetic field region because the magnetic force acts perpendicular to its velocity, resulting in no change in speed and hence no change in kinetic energy.
- We have a charged particle (with charge q) moving with an initial velocity v and enters a region with a uniform magnetic field B.
- Assume the particle is moving in a direction perpendicular to the magnetic field. For example, if the particle moves in the positive x-direction, the magnetic field can be directed in the negative z-direction.
- The force acting on the charged particle due to the magnetic field is given by the Lorentz force formula:
F=q(v×B)
- Since the velocity v and the magnetic field B are perpendicular, the magnitude of the force can be expressed as:
F=qvB
- The magnetic force acts perpendicular to the velocity of the charged particle. This means that while the particle's direction changes, the speed (magnitude of velocity) remains constant.
- The perpendicular force causes the particle to undergo circular motion. In uniform circular motion, the speed of the particle does not change, only its direction does.
- The kinetic energy KE of the particle is given by:
KE=12mv2
- Since the speed v of the particle remains constant while it is in the magnetic field, the kinetic energy also remains constant.
- According to the work-energy theorem, the work done on the particle is equal to the change in kinetic energy. Since the magnetic force is always perpendicular to the displacement of the particle, the work done by the magnetic force is zero:
W=F⋅d⋅cos(90∘)=0
- Therefore, the change in kinetic energy is also zero:
KEfinal−KEinitial=0
- Since there is no change in kinetic energy, we conclude that a charged particle does not gain kinetic energy when it passes through a magnetic field region.
No, a charged particle does not gain kinetic energy when passed through a magnetic field region because the magnetic force acts perpendicular to its velocity, resulting in no change in speed and hence no change in kinetic energy.
Topper's Solved these Questions
- UNIT–III & UNIT–IV MAGNETIC EFFECTS OF CURRENT AND MAGNETISM & E.M.I. AND ALTERNATING CURRENTBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - UNIT–III & UNIT–IV MAGNETIC EFFECTS OF CURRENT AND MAGNETISM & E.M.I. AND ALTERNATING CURRENTEXERCISE - SHORT ANSWER QUESTIONS (2 Marks)
41 Videos
- UNIT–III & UNIT–IV MAGNETIC EFFECTS OF CURRENT AND MAGNETISM & E.M.I. AND ALTERNATING CURRENTBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - UNIT–III & UNIT–IV MAGNETIC EFFECTS OF CURRENT AND MAGNETISM & E.M.I. AND ALTERNATING CURRENTEXERCISE - SHORT ANSWERS QUESTIONS (3 Marks)
27 Videos
- SAMPLE QUESTION PAPER 2019BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - SAMPLE QUESTION PAPER 2019EXERCISE - Section C
19 Videos
Similar Questions
If an alpha particle and an electron have the same kinetic energy. Which undergoes the greater deflection when passed through a magnetic field?
View SolutionDiscuss the motion of a charged particle when subjected to a uniform magnetic field, when the direction of motion of the particle makes an angle ϕ with the direction of magnetic field.
View Solution
Knowledge Check
the magnetic field shown in the figure consist of the two magnetic fields.
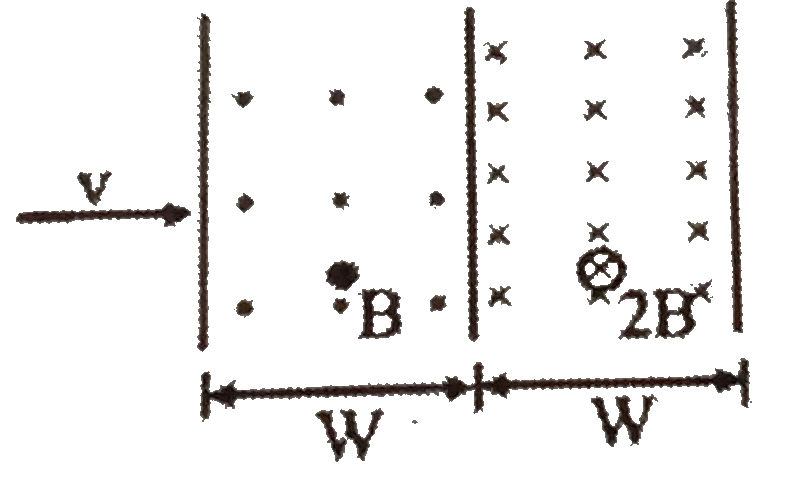
If v is the velocity just required for a charge particles of mass m and charge q to pass through the magnetic field. Particle is projected with velocity 'v' then how much time does such a charge spend in the magntic filed-Aπm2qBBπmqBCπm4qBD3πm2qBWhen a charged particle moves perpendicular to a magnetic field, then:
Aspeed of the particle is changedBspeed of the particle remains unchangedCdirection of the particle remains unchangedDacceleration of the particle remains unchangedWhen a charged particle moves through a magnetic field it suffers a change in its
AenergyBmassCspeedDdirection of motion
A charge q moving along the X-axis with a velocity →v is subjected to a uniform magnetic field B acting along the Z-axis as it crosses the origin O. Figure.
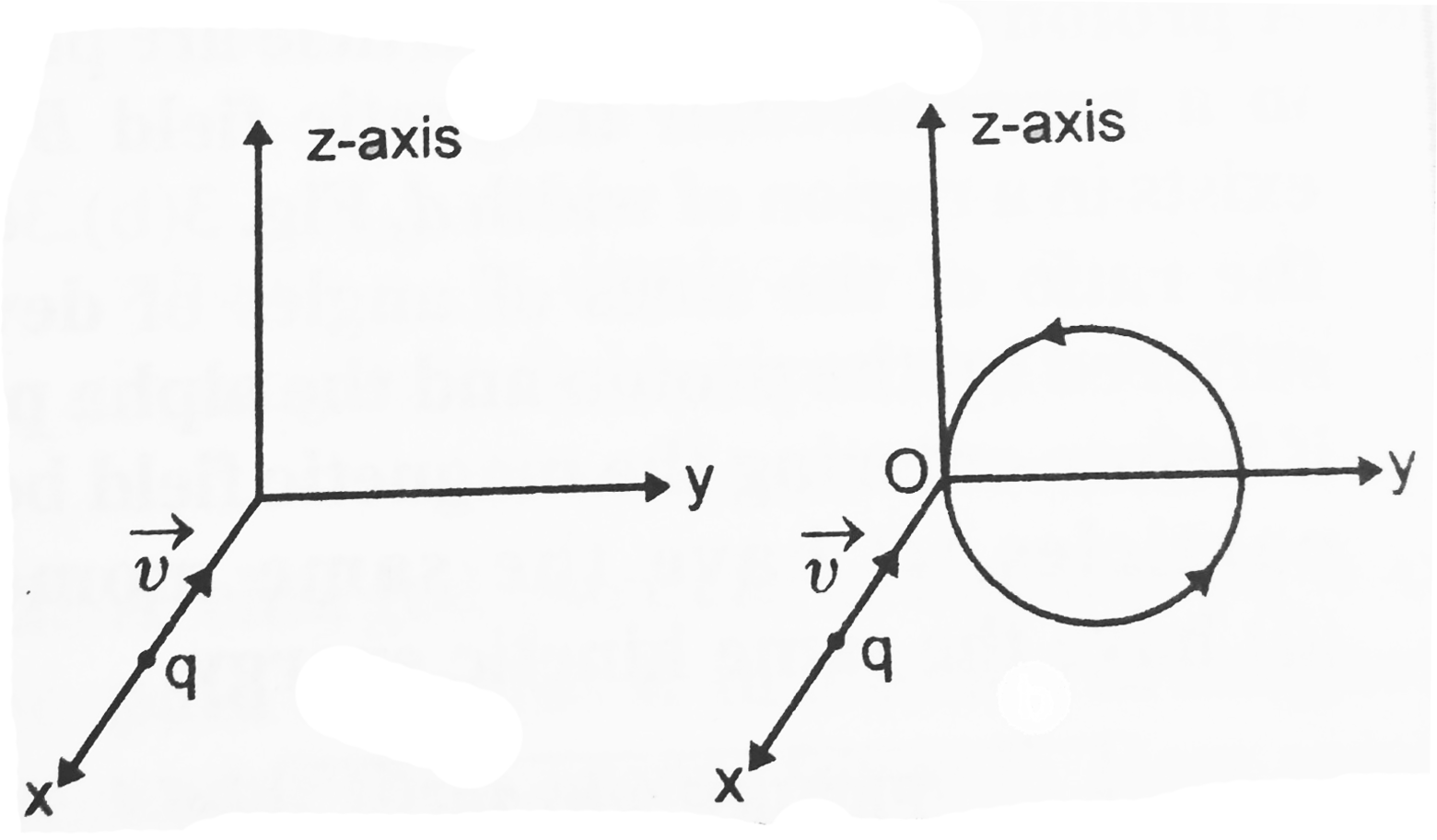
(i) Trace its trajectory . (ii) Does the charge gain kinetic energy as it enters the magnetic field? Justify yous answer.
View SolutionA charge 'q' moving along the X-axis with a velociyt →v (fig) is subjected to a uniform magnetic field →B acting along the Z-axis as it crosses the origin O.
(i) Trace its trajectory.
(ii) Does the charge gain kinetic energy as it enters the magnetic field? Justify your answer.
View SolutionWhen a charged particle moves perpendicular to a magnetic field, then:
View SolutionWhen a charged particle moves through a magnetic field , the quantity which is not affected in the magnetic field is
View SolutionWhen a charged particle moves through a magnetic field , the quantity which is not affected in the magnetic field is
View Solution
