Two blocks P and Q of masses 0.3 kg and 0.4 kg respectively are stuck to each other by some weak glue as shown in the figure. They hand together at the end of a spring with a spring constant k = 200 N m−1. The block Q suddenly falls free due to failure of glue, then find the maximum kinetic energy of the block P during subsequent motion (in mJ).

The correct Answer is:40
Step by step video, text & image solution for Two blocks P and Q of masses 0.3 kg and 0.4 kg respectively are stuck to each other by some weak glue as shown in the figure. They hand together at the end of a spring with a spring constant "k = 200 N m"^(-1). The block Q suddenly falls free due to failure of glue, then find the maximum kinetic energy of the block P during subsequent motion (in mJ). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions

A block of mass 200 g is given velocity 2(m)/(s) on a horizontal surface as shown in the figure. Find the maximum compression of spring of spring constant k=100(N)/(m)View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
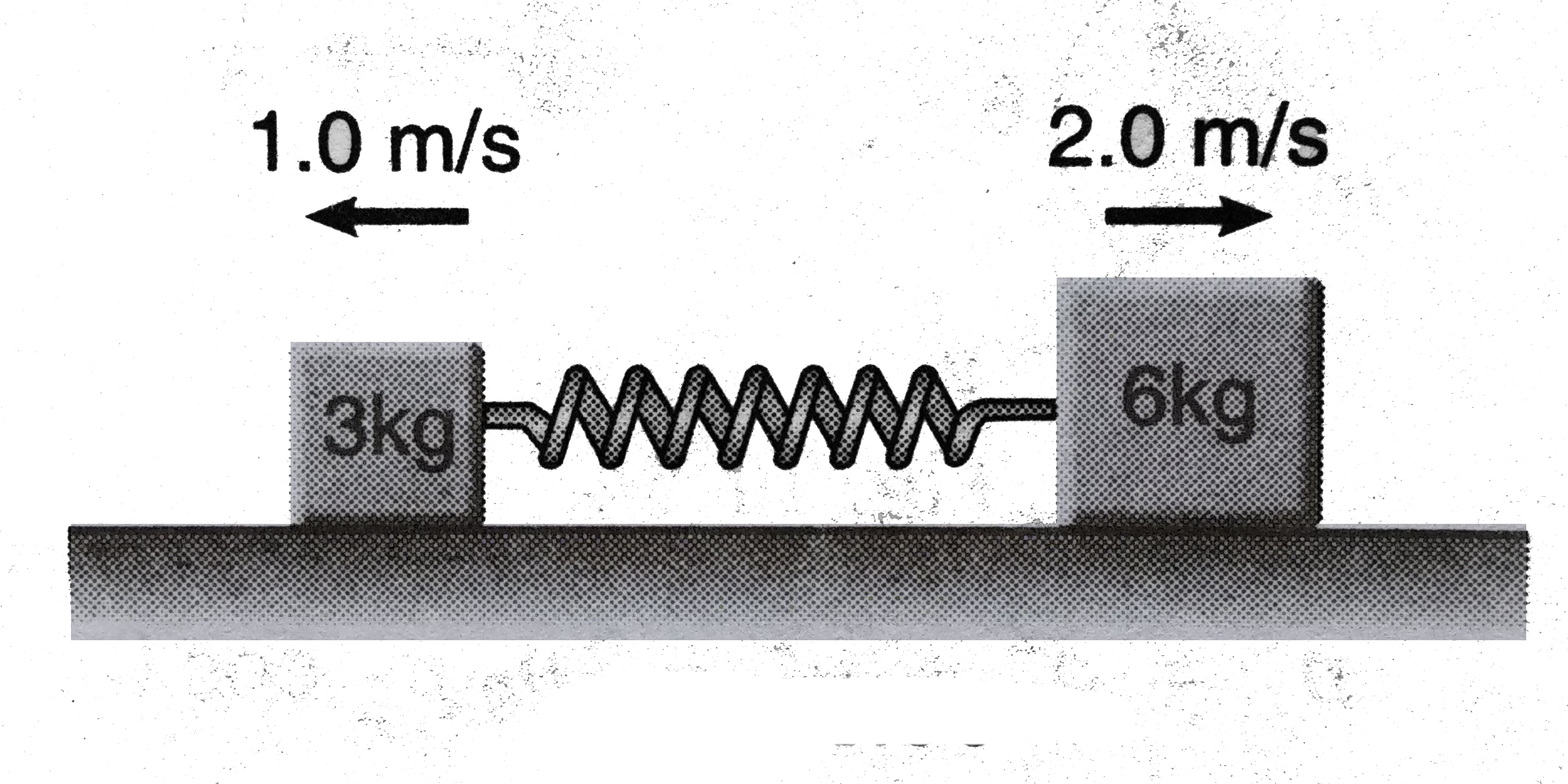 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
Two blocks are connected to the two free ends of a spring of spring constant K . Both the blocks are moved apart to extend the psring beyond its natural length and then released . In subsequent motion
AAccelerations of both the objects are equal and opposite of each other .BVelocities of both the bjects are equal and opposite of each other .CForces acting on both the objects are equal and opposite of each otherDLinear momenta of both the objects are equal and opposite of each other . - Question 2 - Select One
Two block of mass 4 kg and 5 kg attached a light spring are suspended by a string as shown in figure. Find acceleration of block 5 kg and 4 kg just after the string is cut.
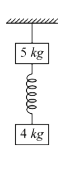 A8m/s2,10m/s2B10m/s2,10m/s2C18m/s2,0D8m/s2,0
A8m/s2,10m/s2B10m/s2,10m/s2C18m/s2,0D8m/s2,0 - Question 3 - Select One
A 0.25kg block oscillates on the end of the spring with a spring constant of 200N/m. If the oscillation is started by elongating the spring 0.15m and giving the block a speed of 3.0m/s, then the maximum speed of the block is
A0.13m/sB0.18m/sC3.7m/sD5.2m/s
Two blocks of mass 2kg and 5kg are given speed as shown in the figure. System is lying on a frictionless surface and the blocks are connected by a massless spring if spring constant 35Nm. Find the maximum compression in the spring.
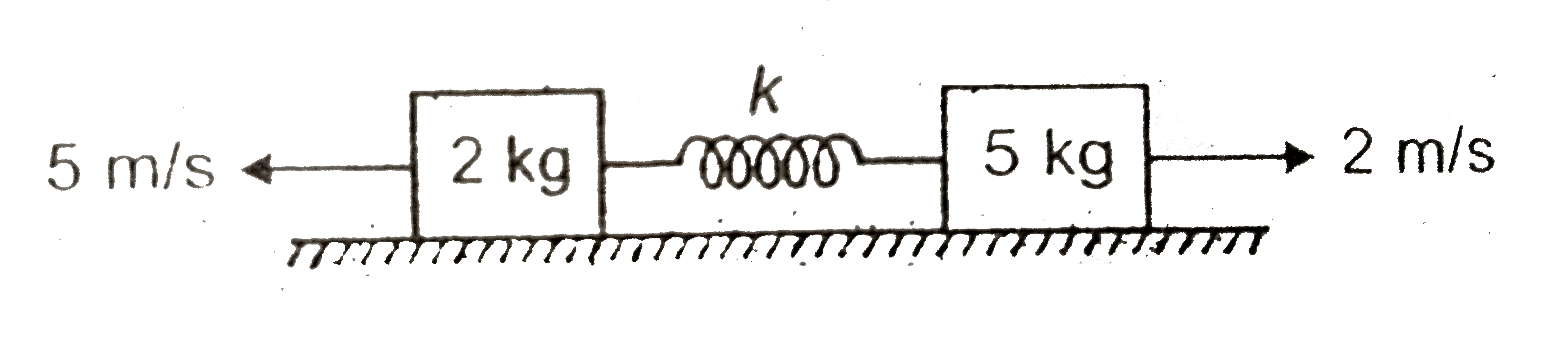 View Solution
View SolutionTwo block A and B of masses m1=3kg and m2=6kg respectively are connected with each other by a spring of force constant k=200N/m as shown in figure. Blocks are pulled away from each other by x0=3cm and then released. When spring is in its natural length and block are moving towards each other, another block C of mass m=3kg moving with velocity v0=0.4m/s (towards right) collides with A and gets stuck to it. Neglecting friction, calculate

(a) velocity v1 and v2 of the blocks A and B respectively just before collision and their angular frequency .
(b) velocity of centre of mass of the system, after collision,
( c) amplitude of oscillation of combined body,
(d) loss of energy during collision.View SolutionA block attached with an ideal spring is kept on a smooth horizontal surface. Now the free end of the spring is pulled with a constant velocity u horizontally. Then the maximum energy stored in the spring and bock system during subsequent motion is :
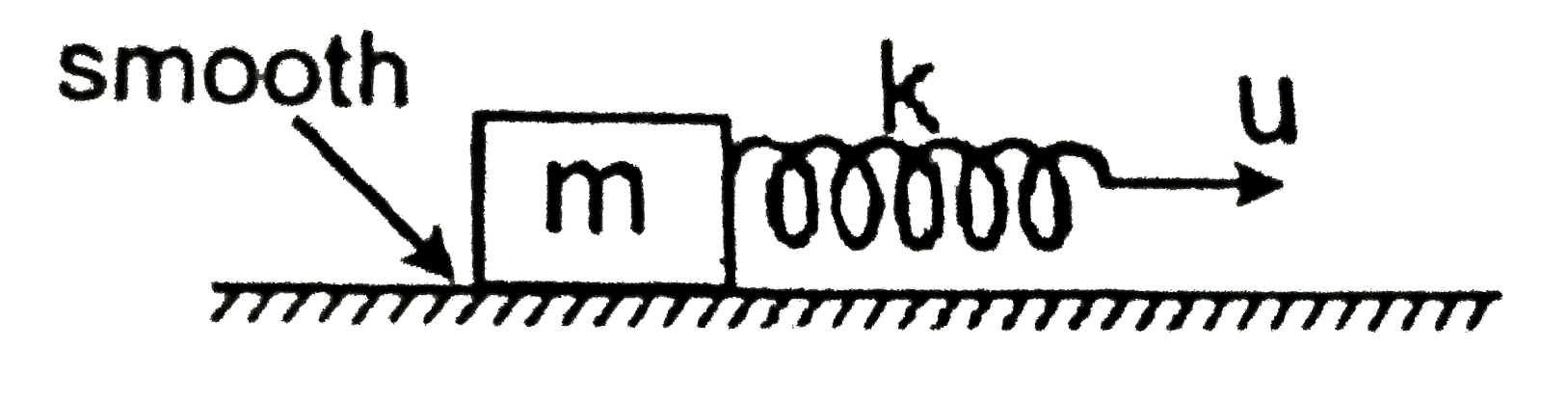 View Solution
View SolutionA block of mass m compresses a spring iof stifffness k through a distacne l/2 as shown in the figure .If the block is not fixed to the spring the period of motion of the block is
 View Solution
View SolutionTwo blocks of masses 6 kg and 3 kg are attached to the two ends of a massless spring of spring constant 2π2N/m. If spring is compressed and released on a smooth horizontal surface then find the time period (in seconds) of each block.
View Solution

