A solid cylinder of radius R & length 3R is made of a metarial having density ρ . Now two hemispheres each of radius R is removed from two ends of cylinder as shown in figure. Determine the moment of inertia of this object about axis of cylinder?

The correct Answer is:5
Step by step video, text & image solution for A solid cylinder of radius R & length 3R is made of a metarial having density rho . Now two hemispheres each of radius R is removed from two ends of cylinder as shown in figure. Determine the moment of inertia of this object about axis of cylinder? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
An infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R2 with its center on the axis of the cylinder, as shown in the figure. The magnitude of the electric field at the point P, which at a distance 2 R (from the axis of the cylinder, is given by the expression 23ρR16nɛ0, The value of n is
'(##CEN_KSR_PHY_JEE_C18_E01_040_Q24##)'View SolutionAn infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electic field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
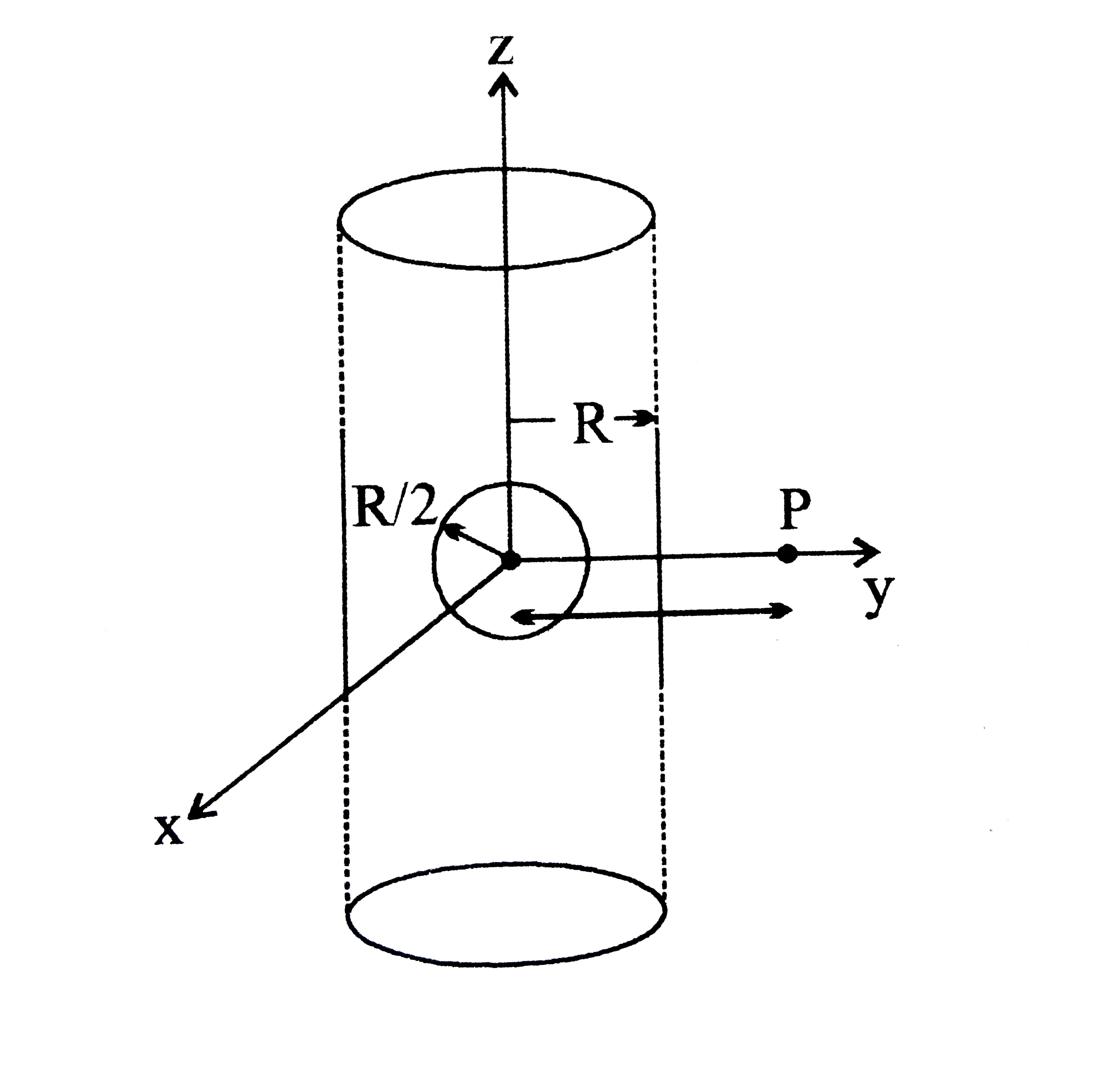 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One

A cylinder of radius R is to roll without slippoing between two planks as shown in the figure. ThenAangular velocity of the cylinder is vR counter clockwiseBangular velocity of the cylinder is 2vR clockwiseCvelocity of centre of mass of the cylinder is v towards leftDvelocity of centre of mass of the cylinder is 2v towards right. - Question 2 - Select One or More
A cylinder of radius R and length l is placed in a uniform electric field E parallel to the axis of the cylinder. The total flux over the curved surface of the cylinder is
AzeroBπR2EC2πR2EDE/πR2 - Question 3 - Select One
The moment of inertia of a solid cylinder of mass M, length 2 R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I, and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2 then
AI2>I1BI2−I1=MR2CI2I1=1912DI2I1=76
Three identical solid discs, each of mass M and radius R, are arranged as shown in figure. The moment of inertia of the system about an axis AB will be
 View Solution
View SolutionAn infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electric field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
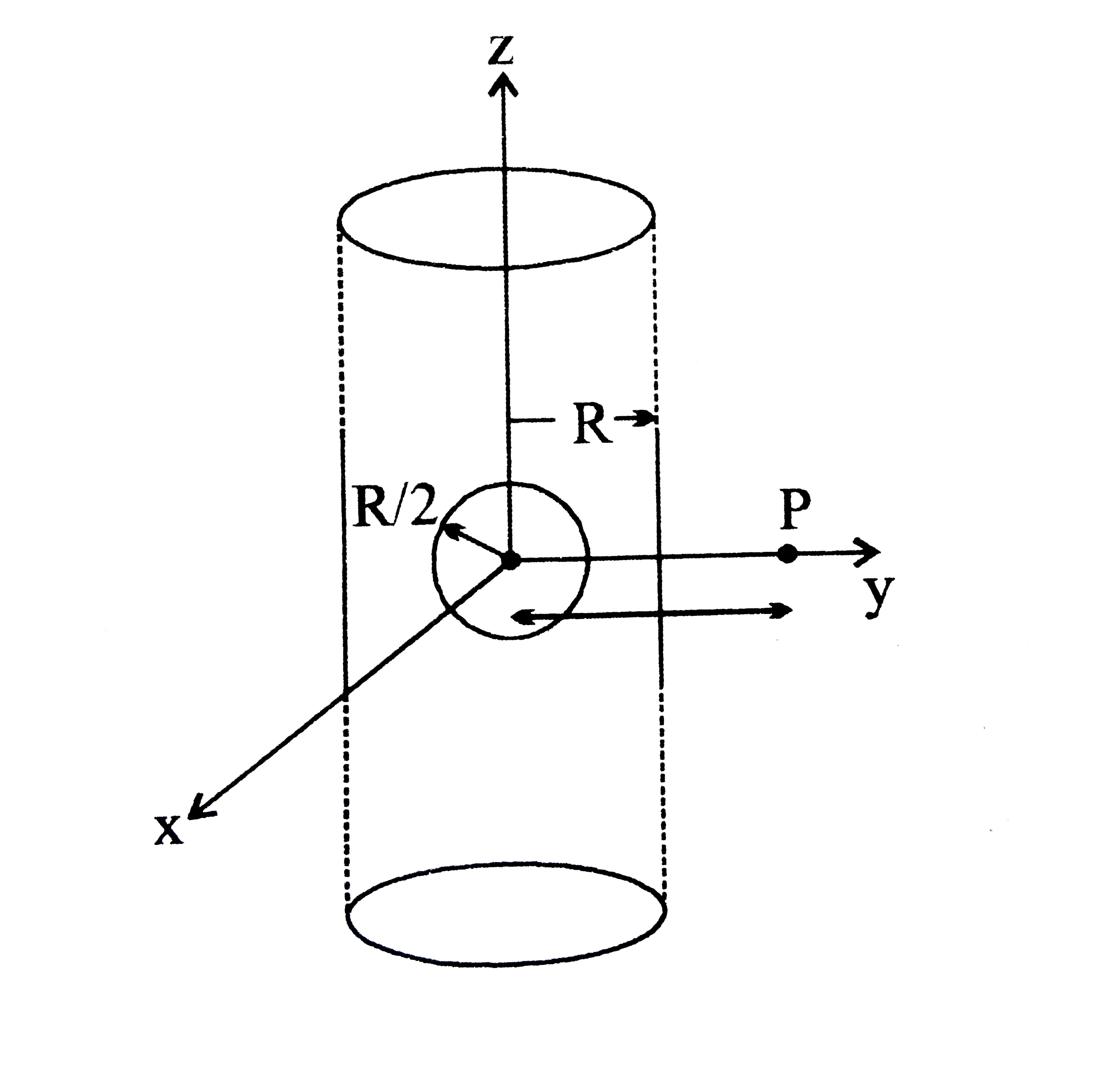 .View Solution
.View SolutionAn infinitely long solid cylinder of radius R with uniform volume charge density ρ has a spherical cavity of radius R2 with its centre on the axis of the cylinder as shown in the figure. The magnitude of the electric field at a point P which is at a distance 2R from the axis of the cylinder is given by 23ρR6Kε0. What is the value of K ?
View SolutionThe mass of the cylinder is 25 kg and radius of cylinder is 5 m. Find the moment of inertia of a solid cylinder about a tangent to the cylinder.
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View Solution

