Let V1= variance of {13,16,19…………103}andV2= variance of {20,26,32…………..200}. Then V1:V2 is
1:2
1:1
4:9
1:4
The correct Answer is:D
To find the ratio of the variances V1:V2 for the given sequences, we will follow these steps:
Step 1: Identify the sequences
The first sequence is S1={13,16,19,…,103} and the second sequence is S2={20,26,32,…,200}.
Step 2: Determine the number of terms in each sequence
For the first sequence S1:
- The first term a1=13
- The common difference d1=3
- The last term an=103
Using the formula for the n-th term of an arithmetic progression (AP):
an=a1+(n−1)d
Setting an=103:
103=13+(n−1)⋅3
103−13=(n−1)⋅3
90=(n−1)⋅3
n−1=30⟹n=31
So, there are 31 terms in S1.
For the second sequence S2:
- The first term a2=20
- The common difference d2=6
- The last term an=200
Using the same formula:
200=20+(n−1)⋅6
200−20=(n−1)⋅6
180=(n−1)⋅6
n−1=30⟹n=31
So, there are also 31 terms in S2.
Step 3: Calculate the variance of each sequence
The variance V of a sequence is given by:
V=1n∑(xi−¯x)2
However, we can also use the property that variance is proportional to the square of the common difference when the number of terms is the same.
For S1:
- The common difference d1=3
- Therefore, V1∝d21=32=9
For S2:
- The common difference d2=6
- Therefore, V2∝d22=62=36
Step 4: Find the ratio of variances
Now, we can find the ratio of the variances:
V1V2=936=14
Final Answer
Thus, the ratio V1:V2 is 1:4.
---
The first sequence is S1={13,16,19,…,103} and the second sequence is S2={20,26,32,…,200}.
For the first sequence S1:
- The first term a1=13
- The common difference d1=3
- The last term an=103
an=a1+(n−1)d
Setting an=103:
103=13+(n−1)⋅3
103−13=(n−1)⋅3
90=(n−1)⋅3
n−1=30⟹n=31
So, there are 31 terms in S1.
- The first term a2=20
- The common difference d2=6
- The last term an=200
200=20+(n−1)⋅6
200−20=(n−1)⋅6
180=(n−1)⋅6
n−1=30⟹n=31
So, there are also 31 terms in S2.
The variance V of a sequence is given by:
V=1n∑(xi−¯x)2
However, we can also use the property that variance is proportional to the square of the common difference when the number of terms is the same.
- The common difference d1=3
- Therefore, V1∝d21=32=9
- The common difference d2=6
- Therefore, V2∝d22=62=36
Now, we can find the ratio of the variances:
V1V2=936=14
Thus, the ratio V1:V2 is 1:4.
Topper's Solved these Questions
Similar Questions
If the variance of the first 50 odd natural numbers is V1 and the variance of next 50 odd natural numbers is V2, then V1+V2 is equal to
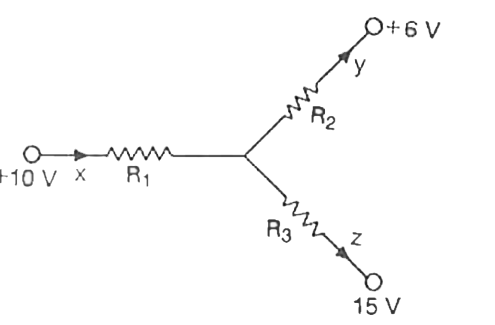
View SolutionFind the currents in the Y connection of 3 resistances R1=10Ω, R2=20Ω and R3=30Ω. When the terminals of R1 , R3 and R3 are maintained at potentials V1 = 10V, V2=6V and V3 = 15V.
View Solution
Knowledge Check
Let Vr denote the sum of first r terms of an arithmetic progression (A.P.) whose first term is r and the common difference is (2r – 1).
Let Tr=Vr+1−Vr−2andQr+1−Tr for r=1,2…….
The sum V1+V2+….+Vn isA112n(n+1)(3n2−n+1)B112n(n+1)(3n2+n+2)C12n(2n2−n+1)D13(2n3−2n+3)If three vectors V1=αi+j+k,V2=i+βj−2k and V3=i+j are coplanar, and V1 and V3 are perpendicular, then the vector V1×V2 is:
A−i+j+2kBi−j+2kC−i+jD2i−2j+kIf the variance of the data 2, 4, 5, 6, 17 is v, then what is the variance of the data 4, 8, 10, 12, 34?
AvB4vCv2D2v
In the given circuit V01 and V02 are -
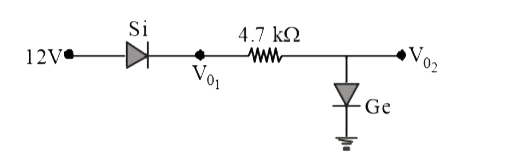
View SolutionIn the figure shows R=100Ω,L=2πH and C=8πμF are connected in series with an a.c. source of 200 volt and frequency f. V1 and V2 are two hot-wire voltmeters. If the reading of V1 and V2 are same, then

View SolutionIf a2+1a2=7andV1andV2 are the minimum and the maximum values of a3+1a3,then V2−V1 is equal to ?
View SolutionVoltmeters V1 and V2 are connected in series across a D.C. line V1 reads 80 volts and has a per volt resistance of 200ohms, V2 has a total resistance of 32 kilo ohms.
The line voltage is
View SolutionIf the variance of the data 2,4,5,6,17 is v1, then what is the variance of the data 4,8,10,12,34 ?
View Solution
