Nucleus A decays into B with a decay constant λ1 and B further decays into C with a decay constant λ2 . Initially, at t = 0, the number of nuclei of A and B were 3N0 and N0 respectively. If at t = t0 number of nuclei of B becomes constant and equal to 2N0, then
t0=1λ1ln[3λ12λ2]
t0=1λ1lm[λ1λ2]
t0=1λ1ln[2λ13λ2]
t0=1λ2ln[3λ12λ2]
The correct Answer is:A
To solve the problem, we need to analyze the decay process of nuclei A and B. Let's break it down step by step.
Step 1: Understand the Decay Process
- Nucleus A decays into B with a decay constant λ1.
- Nucleus B further decays into C with a decay constant λ2.
- Initially, at t=0, the number of nuclei of A is 3N0 and the number of nuclei of B is N0.
Step 2: Write the Rate Equations
The rate of change of the number of nuclei B can be expressed as:
dNBdt=λ1NA−λ2NB
Where:
- NA is the number of nuclei A at time t.
- NB is the number of nuclei B at time t.
Step 3: Express NA and NB
At any time t, the number of nuclei A can be expressed as:
NA(t)=3N0e−λ1t
Initially, NB(0)=N0. To find NB(t), we need to solve the differential equation.
Step 4: Solve the Differential Equation
At t=t0, it is given that NB becomes constant and equal to 2N0. This means:
dNBdt=0at t=t0
Substituting into the rate equation:
0=λ1NA(t0)−λ2NB(t0)
Substituting NA(t0) and NB(t0):
0=λ1(3N0e−λ1t0)−λ2(2N0)
Step 5: Simplify the Equation
Dividing through by N0 (assuming N0≠0):
0=λ1(3e−λ1t0)−2λ2
Rearranging gives:
λ1(3e−λ1t0)=2λ2
Thus,
3e−λ1t0=2λ2λ1
Step 6: Solve for t0
Now, we can express e−λ1t0:
e−λ1t0=2λ23λ1
Taking the natural logarithm of both sides:
−λ1t0=ln(2λ23λ1)
Thus,
t0=−1λ1ln(2λ23λ1)
Step 7: Final Expression
This can be rearranged to:
t0=1λ1ln(3λ12λ2)
Conclusion
The final expression for t0 is:
t0=1λ1ln(3λ12λ2)
- Nucleus A decays into B with a decay constant λ1.
- Nucleus B further decays into C with a decay constant λ2.
- Initially, at t=0, the number of nuclei of A is 3N0 and the number of nuclei of B is N0.
The rate of change of the number of nuclei B can be expressed as:
dNBdt=λ1NA−λ2NB
Where:
- NA is the number of nuclei A at time t.
- NB is the number of nuclei B at time t.
At any time t, the number of nuclei A can be expressed as:
NA(t)=3N0e−λ1t
Initially, NB(0)=N0. To find NB(t), we need to solve the differential equation.
At t=t0, it is given that NB becomes constant and equal to 2N0. This means:
dNBdt=0at t=t0
Substituting into the rate equation:
0=λ1NA(t0)−λ2NB(t0)
Substituting NA(t0) and NB(t0):
0=λ1(3N0e−λ1t0)−λ2(2N0)
Dividing through by N0 (assuming N0≠0):
0=λ1(3e−λ1t0)−2λ2
Rearranging gives:
λ1(3e−λ1t0)=2λ2
Thus,
3e−λ1t0=2λ2λ1
Now, we can express e−λ1t0:
e−λ1t0=2λ23λ1
Taking the natural logarithm of both sides:
−λ1t0=ln(2λ23λ1)
Thus,
t0=−1λ1ln(2λ23λ1)
This can be rearranged to:
t0=1λ1ln(3λ12λ2)
The final expression for t0 is:
t0=1λ1ln(3λ12λ2)
Topper's Solved these Questions
Similar Questions
A radioactive substance A having N0 active nuclei at t=0, decays to another radioactive substance B with decay constant λ1. B further decays to a stable substance C with decay constant λ2. (a) Find the number of nuclei of A,B and C time t. (b) What should be the answer of part (a) if λ1>>λ2 and λ1<<λ2
View SolutionA radioactive nucleus X decays to a nucleus Y with a decay constant λX=0.1s−1, Y further decays to a stable nucleus Z with a decay constant
λY=1/30s−1. Initially, there are only X nuclei and their number is N0=1020. Set up the rate equations for the populations of X, Y and Z. The population of Y nucleus as a function of time is given by NY(t)={N0λX/(λX−λY)}[exp(−λYt)−exp(−λXt)].
Find the time at which NY is maximum and determine the population X and Z at that instant.
View Solution
Knowledge Check
Nucleus A decays to B with decay constant λ1 and B decays to C with decay constant λ2. Initially at t=0 number of nuclei of A and B are 2N0 and N0 respectively. At t=to, no. of nuclei of B is 3N02 and nuclei of B stop changing. Find t0?
A1λ1ln(2λ13λ2)B1λ1ln(8λ13λ2)C1λ1ln(7λ13λ2)D1λ1ln(4λ13λ2)Two radioactive materials A & B have decay constant 3λ and 2λ respectively. At t=0 the numbers of nuclei of A and B are 4N0 and 2N0 respectively then,
ATheir number of radioactive nuclei will be equal at t=ln2λBTheir decay rate will be equals at t=ln4λCTheir decay rate will be equal at t=ln3λDAt t=ln4λ the decay rate of A will be greater than that of B.A radioactive element A of decay constant λA decays into another radioactive element B of decay constant λB. Initially the number of active nuclei of A was N0 and B was absent in the sample. The maximum number of active nuclei of B is found at t=2. In 2/λA. The maximum number of active nuclei of B is
AN04BλAλBN0e−λBtCλAλBN04DNone of these
Consider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.

The net rate of accumulation of B at any instant is
View SolutionConsider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
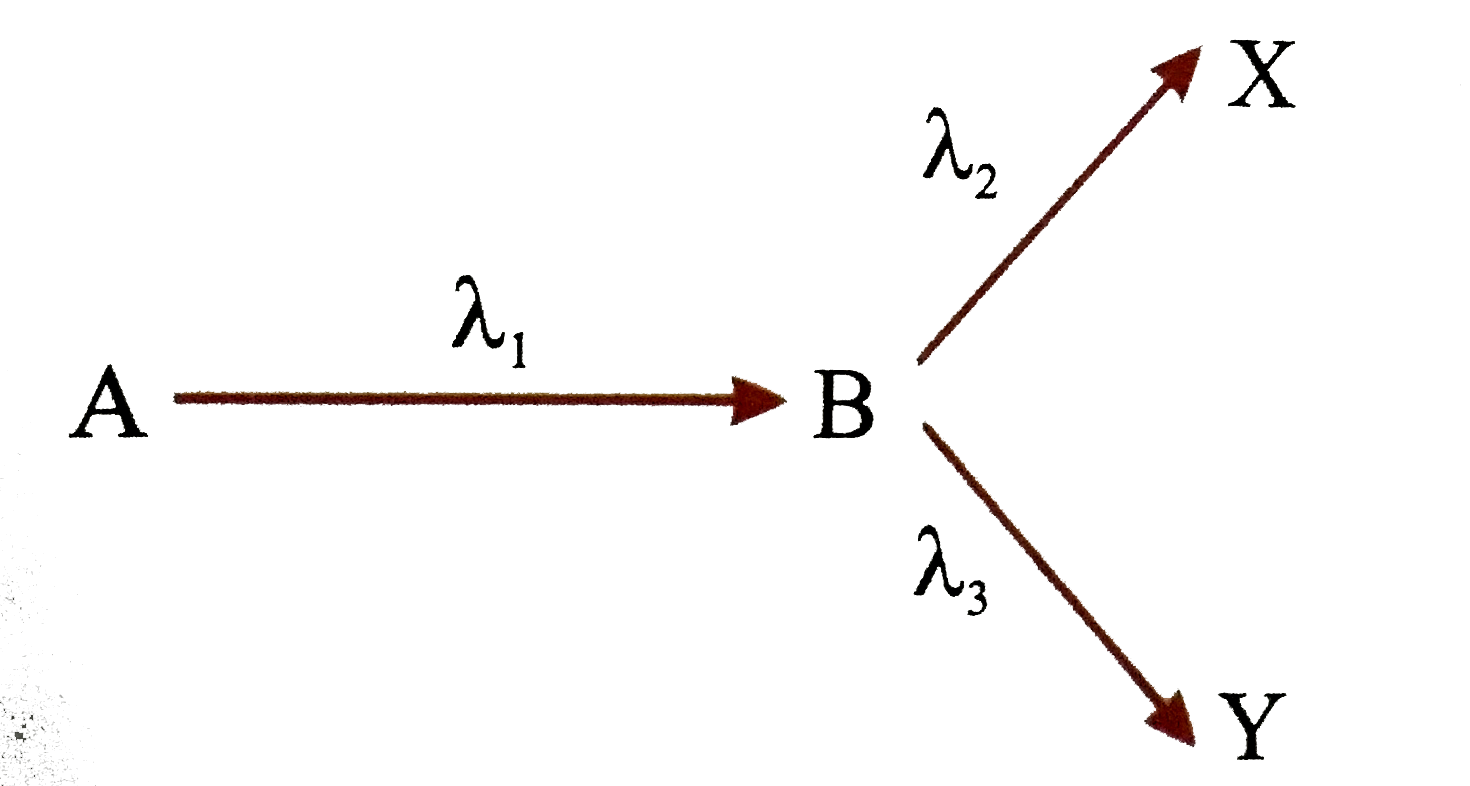
At t=∞, which of following is incorrect ?
View SolutionConsider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
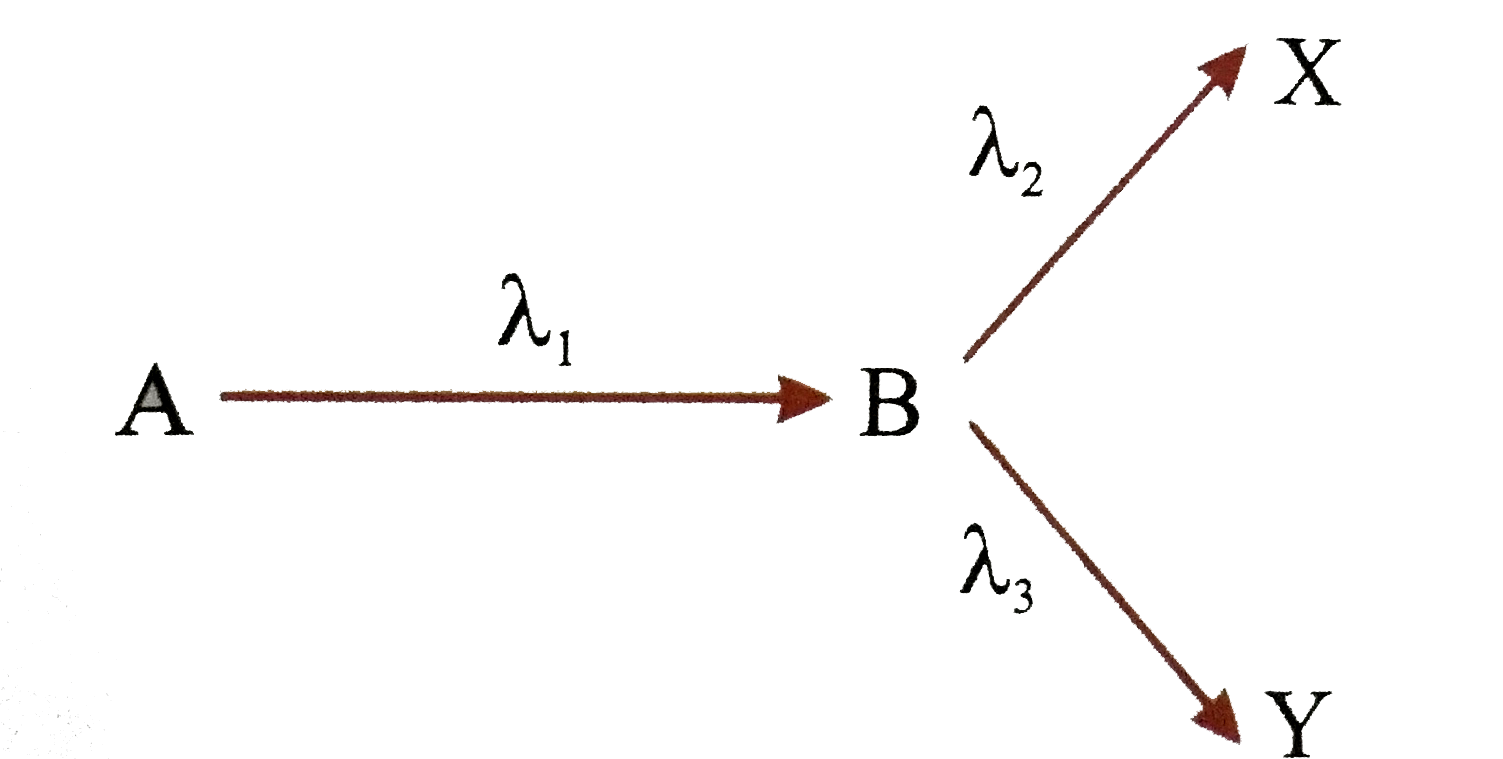
The number of nuclei of B will first increase and then after a maximum value, it decreases for
View SolutionA parent radioactive nucleus A (decay constant λA) converts into a radio-active nucleus B of decay constant λb, initially, number of atoms of B is zero At any time Na,Nb are number of atoms of nuclei A and B respectively then maximum velue of Nb.
View SolutionAt time t=0N1 nuclei of decay constant λ1&N2 nuclei of decay constant λ2 are mixed. The decay rate of the mixture at time 't' is:
View Solution
