A uniform smooth rod (mass m and length l) placed on a smooth horizontal floor is hit by a particle (mass m) moving on the floor, at a distance l4 from one end elastically (e=1). The distance travelled by the centre of the rod after the collision when it has completed three revolutions will be
2πl
3πl
πl
4πl
The correct Answer is:A
Step by step video, text & image solution for A uniform smooth rod (mass m and length l) placed on a smooth horizontal floor is hit by a particle (mass m) moving on the floor, at a distance l/4 from one end elastically (e = 1). The distance travelled by the centre of the rod after the collision when it has completed three revolutions will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
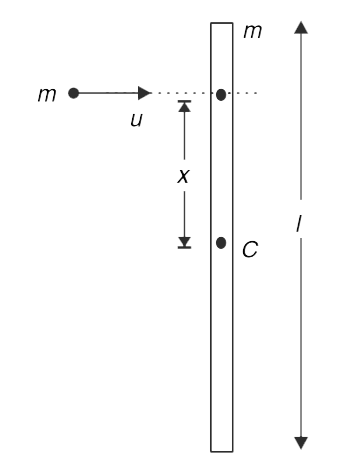
A uniform rod of mass m and length l has been placed on a smooth table A particle of mass m, travelling perpendicular to the rod, hits it at a distance x=l√6 from the centre C of the rod. Collision is elastic.
(a) Find the speed of the centre of the rod and the particle after the collision.
(b) Do you think there is a chance of second Collision? If yes, how is the system of particle and stick moving after the second collision?
 View Solution
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
A3pmlBpmlCp2mlD2pml - Question 2 - Select One
A Iong slender rod of mass 2kg and length m is placed on a smooth horizontal table. Two particles of masses 2kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig.
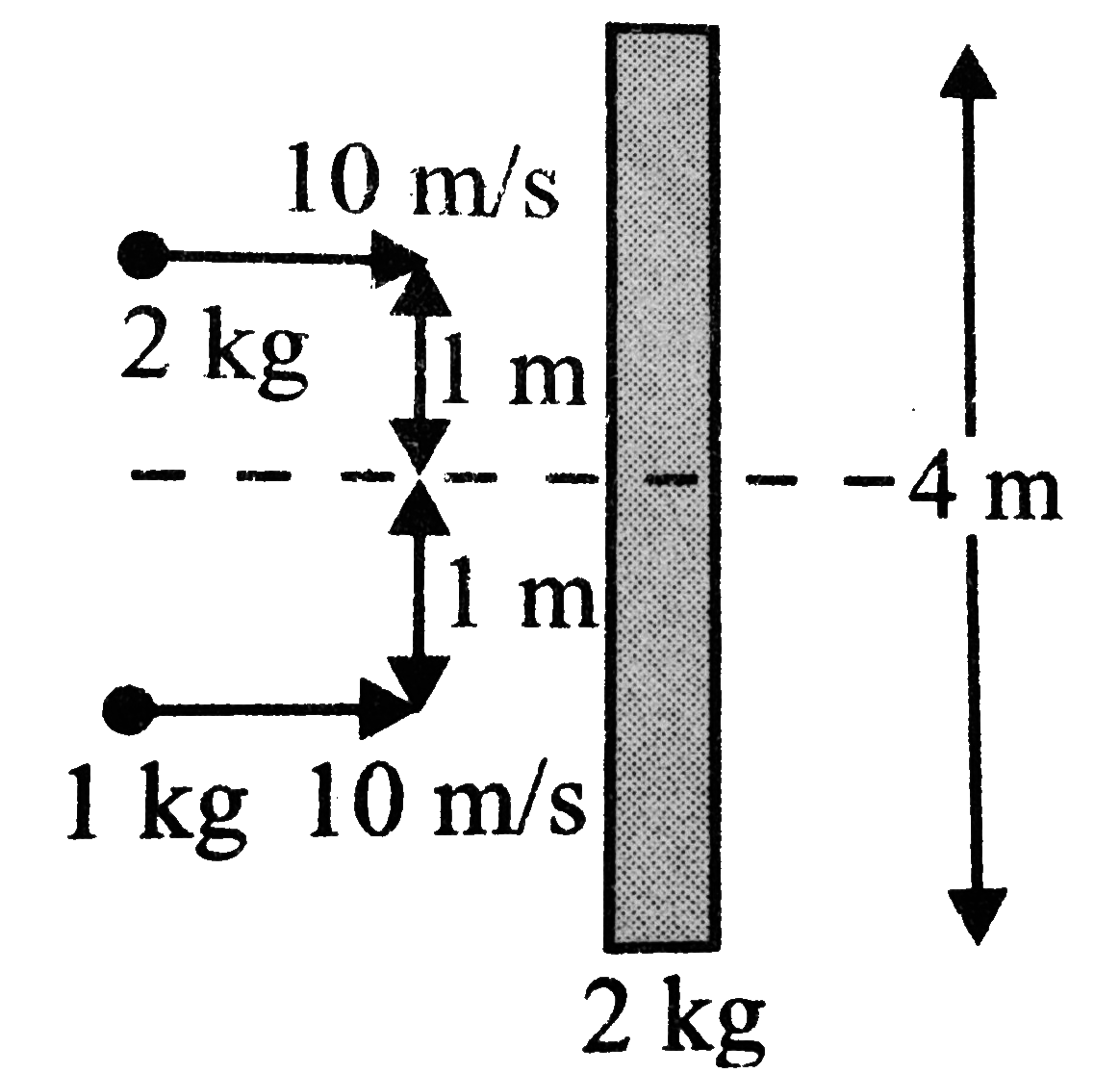
Velocity of the centre of mass of the rod after collision isA12m/sB9m/sC6m/sD3m/s - Question 3 - Select One
A uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B, perpendicular to the rod in the horizontal direction. Speed of particlem P at a distance l6 from the centre towards A of the rod after time t=πml12J is.
A2JmBJ√2mCJmD√2Jm
A uniform rod of length L lies on a smooth horizontal table. A particle moving on the table strikes the rod perpendicularly at an end and stops. Find the distance travelled by the centre of the rod by the time it turns through a right angle. Show that if the mass of the rod is four times that of the particle, the collision is elastic
View SolutionA thin uniform rod of mass M and length L is lying on a smooth horizontal floor. It is struck by a force F normally at one end. The contact lasts for a very small time t0. Find the distance traveled by the rod in the time in which it is turned by π/2.
View SolutionA uniform rod of mass M and length L lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance L/6 from the center and stops after the collision. Find
(a) the velocity of center of mass of rod and
(b) the angular velocity of the rod about its center just after collision.View SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal surface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View Solution

