Consider a horizontal surface moving vertically upward with velocity 2ms−1. A small ball of mass 2 kg is moving with velocity (2ˆi−2ˆj)ms−2 If the coefficient of restitution and coefficient of friction are 12and13 respectively, find the horizontal velocity (in ms−1) of the ball after the collision.
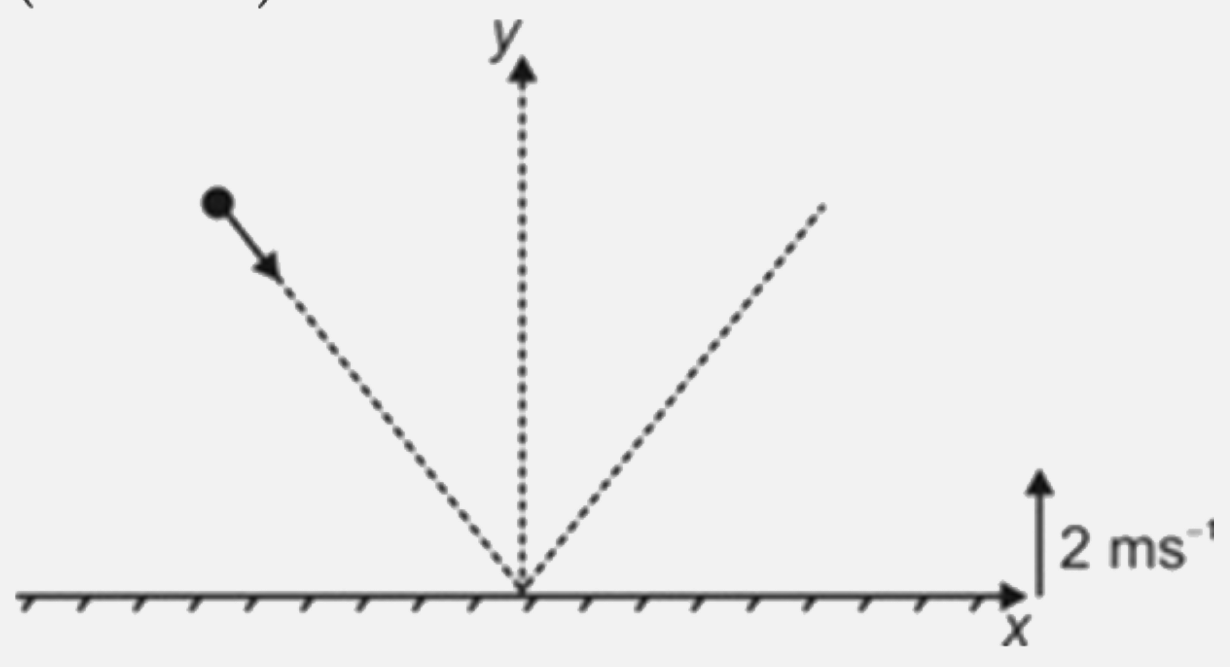
The correct Answer is:0
Step by step video & image solution for Consider a horizontal surface moving vertically upward with velocity 2ms^(-1). A small ball of mass 2 kg is moving with velocity (2hati-2hatj)ms^(-2) If the coefficient of restitution and coefficient of friction are (1)/(2) and (1)/(3 respectively, find the horizontal velocity ("in "ms^(-1)) of the ball after the collision. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
A body of mass 1000 kg is moving horizontally with a velocity 50 ms−1. A mass of 250 kg is added. Find the final velocity.
A40ms−1B23ms−1C12ms−1D12.5ms−1A marble block of mass 2 kg lying on ice when given a velocity of 6ms−1 is stopped by friction in 10 s. Then the coefficient of friction is (g=10ms−2)
A0.02B0.03C0.06D0.01A ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
Av1=(1−e)u2,v2=(1+e)u2Bv1=(1+e)u2,v2=(1−e)u2Cv1=u2,v2=−u2Dv1=(1+e)u,v2=(1−e)u
A ball of mass 25 g, moving with a velocity of 2ms−1 is stopped within 5 cm. The average resistance offered to the ball is
View SolutionA particle of mass m moving with a velocity (3ˆi+2ˆj)ms−1 collides with another body of mass M and finally moves with velocity (−2ˆi+ˆj)ms−1. Then during the collision
View SolutionA shell of mass 10 kg is moving with a velocity with a velocity of 10ms−1 when it blasts and forms two parts of mass 9 kg and 1 kg respectively. If the 1st mass is stationary, the velocity of the 2nd is
View SolutionA truck moving on horizontal road east with velocity 20ms–1 collides elastically with a light ball moving with velocity 25ms–1 along west. The velocity of the ball just after collision
View SolutionA truck moving on horizontal road towards east with velocity 20ms1 collides elastically with a light ball moving with velocity 25ms−1 along west. The velocity of the ball just after collision
View Solution
