A uniform rod of mass m and length L is hinged at one of its end with the ceiling and another end of the rod is attached with a thread which is attached with the horizontal ceiling at point P. If one end of the rod is slightly displaced horizontally and perpendicular to the rod and released. If the time period of small oscillation is 2π√2lsinθxg . Find x.

The correct Answer is:3
Step by step video & image solution for A uniform rod of mass m and length L is hinged at one of its end with the ceiling and another end of the rod is attached with a thread which is attached with the horizontal ceiling at point P. If one end of the rod is slightly displaced horizontally and perpendicular to the rod and released. If the time period of small oscillation is 2pisqrt((2lsintheta)/(xg)) . Find x. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
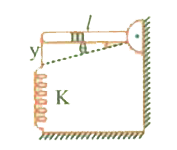
The end of the rod which is connected to the spring is pushed down and released. Find time period of oscillation of the rod ?
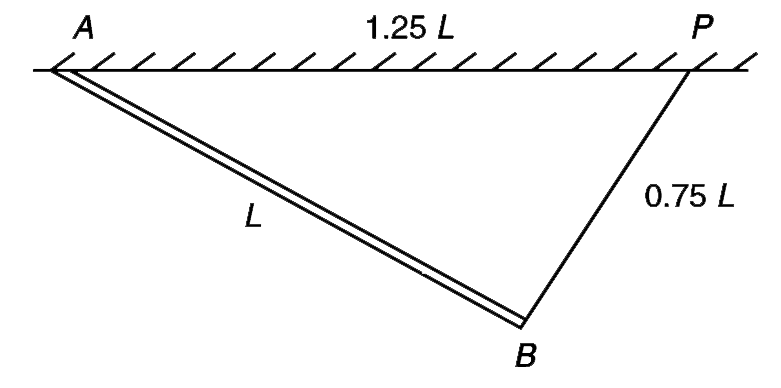
View SolutionA uniform rod AB of mass m and length L is tied, at its end B, to a thread which is attached to point P on the ceiling. Length of the thread PB is 0.75 L. The other end A of the rod is hinged at a point on the ceiling. Distance AP = 1.25 L. End B of the rod is pushed gently perpendicular to the plane of the figure and it starts oscillating
(a) Find the moment of inertia of the rod about line AP.
(b) Assuming that the triangle APB makes a small angle θ with the vertical plane, write the restoring torque acting on the rod.
(c ) Calculate the time period of small oscillations.
View Solution
Knowledge Check
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3gThere is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
AT=2π√2l3gBT=π√l3gCT=2π√l3gDT=2π√lgA rod of mass m and length l is hinged at 'its' end and released from rest in position shown. Find the force exerted by the hinge when the rod becomes horizontal
 Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14
Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14
A uniform rod of mass m and length l is struck at an end by a force F perpendicular to the rod for a short time interval t. Calculate
the kinetic energy of the rod and
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is ω. The force applied on the rod by the pivot is
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is

View SolutionA uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
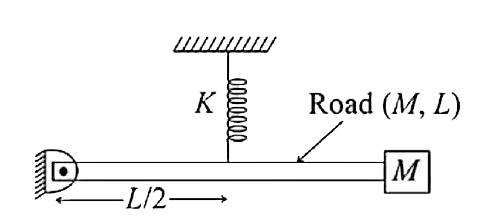
View SolutionA rod of mass 'M' and length'
L' is hinged about one end and a
particle of mass 'M' is
attached to its other end If it is
kept horizontal with the help of
a spring of spring constant 'K'
as shown in fig. find the
extension in spring :-
View Solution